相关习题
0 147186 147194 147200 147204 147210 147212 147216 147222 147224 147230 147236 147240 147242 147246 147252 147254 147260 147264 147266 147270 147272 147276 147278 147280 147281 147282 147284 147285 147286 147288 147290 147294 147296 147300 147302 147306 147312 147314 147320 147324 147326 147330 147336 147342 147344 147350 147354 147356 147362 147366 147372 147380 266669
科目:
来源:山东省胜利一中2006—2007学年度第一学期高三月考数学(文)
题型:044
|
|
解答题:解答应写出文字说明、证明过程或演算步骤
对定义域分别是Df,Dg的函数y=f(x),y=g(x),规定:函数  且 且
| (1) |
|
若函数 写出函数h(x)的解析式 写出函数h(x)的解析式
|
|
(2) |
|
(3) |
|
若g(x)=f(x+α)其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x)及一个α的值,使得h(x)=cos4x,并予以证明.
|
|
|
查看答案和解析>>
科目:
来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(文科)
题型:044
|
|
解答题:解答时要求写出必要的文字说明或推演步骤.
已知向量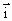 =(1,0), =(1,0),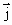 =(0,1),规定 =(0,1),规定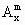 =x(x-1)……(x-m+1),其中x∈R,m∈N+,且 =x(x-1)……(x-m+1),其中x∈R,m∈N+,且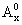 =1.函数f(x)= =1.函数f(x)=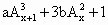 (ab≠0)在x=1处取得极值,在x=2处的切线平行向量 (ab≠0)在x=1处取得极值,在x=2处的切线平行向量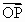 =(b+5,5a). =(b+5,5a).
| (1) |
|
(2) |
|
(3) |
|
是否存在正整数m,使得方程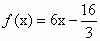 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由. 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
|
|
|
查看答案和解析>>
科目:
来源:山东省临沂市临沭一中2007届高三数学理科12月月考试卷
题型:044
|
|
解答题:解答应写出文字说明,证明过程或演算步骤.
已知  是偶函数. 是偶函数.
| (1) |
|
(2) |
|
证明:对任意实数b,函数y=f(x)的图象与直线 最多只有一个交点 最多只有一个交点
|
|
(3) |
|
设 ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围. ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
|
|
|
查看答案和解析>>
科目:
来源:山东省临祈市2006—2007学年度上学期高三年级期中统一考试 数学试题(理)
题型:044
|
|
解答题:解答应写出文字说明,证明过程或演算步骤.
已知两个二次函数:y=f(x)=ax2+bx+1与y=g(x)=a2x2+bx-1(a>0),函数y=g(x)的图像与x轴有两个交点,其交点横坐标分别为x1,x2(x1<x2)
| (1) |
|
(2) |
|
当a>1时,设x3,x4是方程ax2+bx+1=0的两实根,且x3>x4,试判断x1,x2,x3,x4的大小关系
|
|
|
查看答案和解析>>
科目:
来源:福建省厦门市内厝中学2007届高三月考数学(文)试卷
题型:044
|
|
解答题:解答应写出必要的文字说明、证明过程及演算步骤
二次函数f(x)满足 且f(0)=1. 且f(0)=1.
| (1) |
|
(2) |
|
在区间 上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围. 上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
|
|
|
查看答案和解析>>
科目:
来源:东北育才学校07届高三一轮复习单元测试卷、数学(数列)
题型:044
|
|
解答题
(文科做)设无穷等差数列{an}的前n项和为Sn.
| (1) |
|
(2) |
|
求所有的无穷等差数列{an},使得对于一切正整数k都有 成立. 成立.
|
|
|
查看答案和解析>>
科目:
来源:潮阳一中2007届高三摸底考试、文科数学
题型:044
|
|
解答题
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称. 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
| (1) |
|
(2) |
|
若Q是双曲线C上的任一点,F1、F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程.
|
|
(3) |
|
设直线y=mx+1与双曲线C的左支交于A、B两点,另一直线L经过M(-2,0)及AB的中点,求直线L在y轴上的截距b的取值范围.
|
|
|
查看答案和解析>>
科目:
来源:潮阳一中2007届高三摸底考试、理科数学
题型:044
|
|
解答题
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称. 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
| (1) |
|
(2) |
|
若Q是双曲线C上的任一点,F1、F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程.
|
|
(3) |
|
设直线y=mx+1与双曲线C的左支交于A、B两点,另一直线L经过M(-2,0)及AB的中点,求直线L在y轴上的截距b的取值范围.
|
|
|
查看答案和解析>>
科目:
来源:北京九中2006-2007学年度第一学期高三期中数学统练试题(理科)
题型:044
|
|
解答题:解答时应写出文字说明、证明过程或演算步骤.
已知函数 的图象都过点P(2,0),且在点P处有相同的切线. 的图象都过点P(2,0),且在点P处有相同的切线.
| (1) |
|
(2) |
|
设函数F(x)=f(x)+g(x),求函数 的极值. 的极值.
|
|
|
查看答案和解析>>
科目:
来源:湖北省钟祥一中2012届高三5月适应性考试(三)数学理科试题
题型:044
设△ABC的内角A、B、C的对边分别为a、b、c,cos(A-C)+cosB= ,b2=ac,求B.
,b2=ac,求B.
查看答案和解析>>

![]() ,b2=ac,求B.
,b2=ac,求B.