已知函数f(x)＝x²－ac－aln(x－1)(a∈R)

(1)当a＝1时，求函数f(x)的最值；

(2)求函数f(x)的单调区间；

(3)试说明是否存在实数a(a≥1)使y＝f(x)的图象与无公共点．

某分公司经销某品牌产品每件产品成本3元，且每件产品需向总公司交a元(3≤a≤5)的管理费，预计当每件产品的售价为x元(9≤x≤11)时，一年的销售量为(12－x)²万件．

(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式；

(2)当每件产品的售价为多少元时，分公司一年的利润L最大，并求出L的最大值Q(a)

记关于x的不等式的解集为P，不等式|x－1|≤1的解集为Q，

(1)若a＝3，求P∪Q．

(2)若QP，求实数a的取值范围．

已知椭圆过点(0，1)，且离心率为．

(Ⅰ)求椭圆C的方程；

(Ⅱ)A，B为椭圆C的左右顶点，直线l：x＝2与x轴交于点D，点P是椭圆C上异于A，B的动点，直线AP，BP分别交直线l于E，F两点．证明：当点P在椭圆C上运动时，|DE|·|DF|恒为定值．

如图，已知菱形ABCD的边长为6，∠BAD＝60°，AC⊥BD＝O．将菱形ABCD沿对角线AC折起，使BD＝3，得到三棱锥B－ACD．

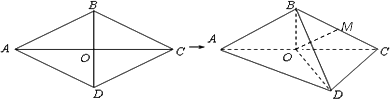
(Ⅰ)若点M是棱BC的中点，求证：OM∥平面ABD；

(Ⅱ)求二面角A－BD－O的余弦值；

(Ⅲ)设点N是线段BD上一个动点，试确定N点的位置，使得CN＝4，并证明你的结论．

已知双曲线的离心率为2，焦点到渐近线的距离等于，过右焦点F₂的直线l交双曲线于A、B两点，F₁为左焦点，

(Ⅰ)求双曲线的方程；

(Ⅱ)若△F₁AB的面积等于6，求直线l的方程．

如图，等腰梯形ABCD中，2BC＝AD＝3，过B作AD的垂线，垂足为O，且OB＝BC，沿着垂线OB将△AOB折起，使平面AOB⊥平面OBCD

(1)证明：平面AOC⊥平面ABC

(2)若E是AD中点，求四面体A＝OCE的体积

设函数f(x)＝x－a(x＋1)ln(x＋1)，a＞0．

(1)求f(x)的单调区间；

(2)证明：．

若存在实数k和b，使得函数f(x)与g(x)对其定义域上的任意实数x分别满足：f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为f(x)与g(x)的“和谐直线”．已知h(x)＝x²，(x)＝2elnx，(e为自然对数的底数)；

(1)求F(x)＝h(x)－(x)的极值；

(2)函数h(x)和(x)是否存在和谐直线？若存在，求出此和谐直线方程；若不存在，请说明理由．

已知f(x)＝a^x－1－1，(a＞1)的反函数为f^－1(x)．

(1)若函数在区间(m，＋∞)上单增，求实数m的取值范围；

(2)若关于x的方程f^－1(x－1)·[f^－1(x－1)－p]＝－2在(1，＋∞)内有两个不相等的实数根，求实数p的取值范围．