质检部门将对12个厂家生产的婴幼儿奶粉进行质量抽检，若被抽检厂家的奶粉经检验合格，则该厂家的奶粉即可投放市场；若检验不合格，则该厂家的奶粉将不能投放市场且作废品处理．假定这12个厂家中只有2个厂家的奶粉存在质量问题(即检验不能合格)，但不知道是哪两个厂家的奶粉．

(Ⅰ)从中任意选取3个厂家的奶粉进行检验，求至少有2个厂家的奶粉检验合格的概率；

(Ⅱ)每次从中任意抽取一个厂家的奶粉进行检验(抽检不重复)，求恰好在第二次抽检到合格奶粉的概率．

已知函数f(x)＝ln(e^x＋a)(a＞0)．

(1)求函数y＝f(x)的反函数y＝f^－1(x)及f(x)的导数

(2)假设对任意x∈[ln(4a)]，不等式|m－f^－1(x)|＋ln((x))＜0成立，求实数m的取值范围．

设函数f(x)定义在R上，对于任意实数m，n，总有f(m＋n)＝f(m)f(n)，且当x＞0时，0＜f(x)＜1．

(1)证明：f(0)＝1，且x＜0时f(x)＞1

(2)证明：函数在R上单调递减

(3)设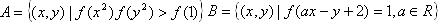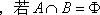，确定a的取值范围．

如图，已知ABCD－A₁B₁C₁D₁是棱长为3的正方体，点E在AA₁上，点F在CC₁上，且AE＝FC₁＝1．

(1)求证：E，B，F，D₁四点共面；

(2)若点G在BC上，

如图，在六面体ABCD－A₁B₁C₁D₁中，四边形ABCD是边长为2的正方形，四边形A₁B₁C₁D₁是边长为1的正方形，DD₁⊥平面A₁B₁C₁D₁，DD₁⊥平面ABCD，DD₁＝2．

(Ⅰ)求证：A₁C₁与AC共面，B₁D₁与BD共面．

(Ⅱ)求证：平面A₁ACC₁⊥平面B₁BDD₁；

(Ⅲ)求二面角A―BB₁―C的大小(用反三角函数值表示)．

已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1．

(1)求椭圆C的标准方程；

(2)若直线l：y＝kx＋m与椭圆C相交于A，B两点(A，B不是左右顶点)，且以AB为直径的图过椭圆C的右顶点．求证：直线l过定点，并求出该定点的坐标．

如图，直线l₁和l₂相交于点M，l₁⊥l₂，点N∈l₁．以A、B为端点的曲线段C上的任一点到l₂的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|＝，|AN|＝3，且|BN|＝6．建立适当的坐标系，求曲线C的方程．

如图，已知A、B、C是长轴为4的椭圆上三点，点A是长轴的一个顶点，BC过椭圆中心O，且．

(1)建立适当的坐标系，求椭圆方程；

(2)如果椭圆上两点P、Q使直线CP、CQ与x轴围成底边在x轴上的等腰三角形，是否总存在实数？请给出证明．

学校科技小组在计算机上模拟航天器变轨返回试验．设计方案如图：航天器运行(按顺时针方向)的轨迹方程为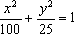，变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、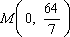为顶点的抛物线的实线部分，降落点为D(8，0)．观测点A(4，0)、B(6，0)同时跟踪航天器．

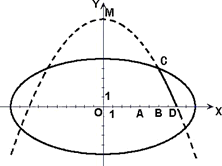
(1)求航天器变轨后的运行轨迹所在的曲线方程；

(2)试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为多少时，应向航天器发出变轨指令？
　

已知函数f(x)＝lnx－ax2＋(2－a)x

(1)讨论f(x)的单调性；(2)设a＞0，证明：当0＜x＜时，f(＋x)＞f(－x)；

(3)若函数y＝f(x)的图象与x轴交于A，B两点，线段AB中点的横坐标为x0，证明(x0)＜0．