设函数y＝f(x)的定义域为(0，＋∞)，且对任意的正实数x，y，均有f(xy)＝f(x)＋f(y)恒成立．已知f(2)＝1，且当x＞1时，f(x)＞0．

(1)求f()的值，试判断y＝f(x)在(0，＋∞)上的单调性，并加以证明；

(2)一个各项均为正数的数列{a_n}，它的前n项和是S_n，若a₁＝3，且f(S_n)＝f(a_n)＋f(a_n＋1)－1(n≥2，n∈N^*)，求数列{a_n}的通项公式；

(3)在(2)的条件下，是否存在实数M，使2ⁿ·a₁·a₂……a_n≥M··(2a₁－1)·(2a₂－1)……(2a_n－1)

对于一切正整数n均成立？若存在，求出M的范围；若不存在，请说明理由．

函数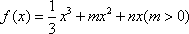在x＝1处取得极值，(x)的最小值为－4．

(1)求m，n的值及f(x)的单调区间；

(2)试分别求方程f(x)－c＝0在区间[－4，1]上有一根、有两根时c的范围．

设函数y＝f(x)的定义域为(0，＋∞)，且对任意的正实数x，y，均有f(xy)＝f(x)＋f(y)恒成立．已知f(2)＝1，且当x＞1时，f(x)＞0．

(1)求的值，试判断y＝f(x)在(0，＋∞)上的单调性，并加以证明；

(2)一个各项均为正数的数列{a_n}，它的前n项和是S_n，若a₁＝3，且对任意的正整数n，均满足，求数列{a_n}的通项公式．

选修4－5：不等式选讲

已知函数f(x)＝|x－2|，g(x)＝－|x＋3|＋m

(1)解关于x的不等式f(x)＋a－1＞0(a∈R)；

(2)若函数f(x)的图象恒在函数g(x)图象的上方，求m的取值范围．

已知函数，

(1)若a＝1，求函数f(x)在点(e，f(e))处的切线方程；

(2)设函数h(x)＝f(x)－g(x)，求函数h(x)的单调区间；

(3)若在[1，e](e＝2.718…)上存在一点x₀，使得f(x₀)＜g(x₀)成立，求a的取值范围．

某种汽车的购车费用是10万元，每年使用的保险费、养路费、汽油费约为0.9万元，年维修费用第一年是0.2万元，第二年是0.4万元，第三年是0.6万元，…，以后逐年递增0.2万元．汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用．设这种汽车使用x(x∈N^*)年的维修费用为g(x)，年平均费用为f(x)．

(1)求出函数g(x)，f(x)的解析式；

(2)这种汽车使用多少年时，它的年平均费用最小？最小值是多少？

已知函数f(x)＝log₂x，设是首项和公差都等于1的等差数列．数列{b_n}满足．

(1)求数列{a_n}的通项公式，并证明数列{b_n}不是等比数列；

(2)令，求证：S_n＜3．

选修4－4：坐标系与参数方程

已知曲线C₁：，曲线C₂：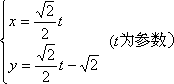

(1)曲线C₁，C₂是否有公共点，为什么？

(2)若把C₁，C₂上各点的横坐标都压缩为原来的一半，分别得到曲线，．问与公共点的个数和C₁与C₂公共点的个数是否相同？说明你的理由．

设x₁、x₂(x₁≠x₂)是函数f(x)＝ax³＋bx²－a²x(a＞0)的两个极值点．

(1)若x₁＝－1，x₂＝2，求函数f(x)的解析式；

(2)若，求b的最大值．

(3)若x₁＜x＜x₂，且x₂＝a，，求证：．

如图，已知椭圆的上顶点为A，右焦点为F，直线AF与圆M：x²＋y²－6x－2y＋7＝0相切．

(Ⅰ)求椭圆C的方程；

(Ⅱ)若不过点A的动直线l与椭圆C相交于P、Q两点，且求证：直线l过定点，并求出该定点N的坐标