对于三次函数f(x)＝ax³＋bx²＋cx＋d(a≠0)．

定义：(1)设(x)是函数y＝f(x)的导数y＝(x)的导数，若方程(x)＝0有实数解x₀，则称点(x₀，f(x₀))为函数y＝f(x)的“拐点”；

定义：(2)设x₀为常数，若定义在R上的函数y＝f(x)对于定义域内的一切实数x，都有f(x₀＋x)＋f(x₀－x)＝2f(x₀)成立，则函数y＝f(x)的图象关于点(x₀，f(x₀))对称．

己知f(x)＝x³－3x²＋2x＋2，请回答下列问题：

(1)求函数f(x)的“拐点”A的坐标

(2)检验函数f(x)的图象是否关于“拐点”A对称，对于任意的三次函数写出一个有关“拐点”的结论(不必证明)

(3)写出一个三次函数G(x)，使得它的“拐点”是(－1，3)(不要过程)

如图，开发商欲对边长为1 km的正方形ABCD地段进行市场开发，拟在该地段的一角建设一个景观，需要建一条道路EF(点E、F分别在BC、CD上)，根据规划要求△ECF的周长为2 km．

(1)设∠BAE＝α，∠DAF＝β，试求α＋β的大小；

(2)欲使△EAF的面积最小，试确定点E、F的位置．

如图，设P是圆x²＋y²＝2上的动点，点D是P在x轴上的投影，M为线段PD上一点，且|PD|＝|MD|．点A(0，)、F₁(－1，0)．

(1)设在x轴上存在定点F₂，使|MF₁|＋|MF₂|为定值，试求F₂的坐标，并指出定值是多少？

(2)求|MA|＋|MF₁|的最大值，并求此时点M的坐标．

如图，四棱锥S－ABCD中，M是SB的中点，AB∥CD，BC⊥CD，且AB＝BC＝2，CD＝SD＝1，又SD⊥面SAB．

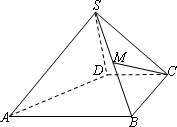
(1)证明：CD⊥SD；

(2)证明：CM⊥面SAD；

(3)求四棱锥S－ABCD的体积．

已知函数f(x)＝·，其中＝(2sinωx，－1)，＝(2sin(－ωx)，1)，ω＞0，f(x)的图象与直线y＝－2的交点的横坐标成公差为π的等差数列

(1)求f(x)的解析式；

(2)若在△ABC中，a＝，b＋c＝3，f(A)＝2，求△ABC的面积．

已知二次函数g(x)对任意实数x都满足g(x)＝g(1－x)，g(x)的最小值为－且g(1)＝－1．令f(x)＝g(x＋)＋mlnx＋(m∈R，x＞0)．

(1)求g(x)的表达式；

(2)若x＞0使f(x)≤0成立，求实数m的取值范围；

(3)设1＜m≤e，H(x)＝f(x)－(m＋1)x，证明：对x₁、x₂∈[1，m]，恒有|H(x₁)－H(x₂)|＜1．

已知数列{a_n}的首项a₁＝，a_n+1＝，n＝1，2，…．

(1)求证：数列为等比数列；

(2)记S_n＝＋＋…，若S_n＜100，求最大正整数n．

(3)是否存在互不相等的正整数m，s，n，使m，s，n成等差数列且a_m－1，a₅－1，a_n－1成等比数列，如果存在，请给出证明；如果不存在，请说明理由．

已知圆C：x²＋y²＋2x－4y＋3＝0；

(1)若圆C的切线在x轴，y轴上的截距相等，求此切线方程；

(2)从圆C外一点P(x₁，y₁)向圆引一条切线，切点为M，O为原点，且有|PM|＝|PO|，求使|PM|最小的P点的坐标．

如图，在半径为30 cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD，其中点A、B在直径上，点C、D在圆周上．

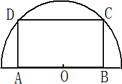
(1)怎样截取才能使截得的矩形ABCD的面积最大？并求最大面积；

(2)若将所截得的矩形铝皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗)，应怎样截取，才能使做出的圆柱形形罐子体积最大？并求最大体积．

设函数f(x)＝a·b，其中向量a＝(m，cos2x)，b＝(1＋sin2x，1)，x∈R，且y＝f(x)的图象经过点(，2)．

(1)求实数m的值；

(2)求f(x)的最小正周期；

(3)求f(x)在[0，]上的单调增区间．