
科目: 来源:浙江省瑞安市十校2012届高三上学期期中联考数学理科试题 题型:044
已知函数f(x)=![]() sinxcos(x+
sinxcos(x+![]() )+
)+![]() .
.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)已知△ABC中,角A,B,C所对的边长分别为a,b,c,若f(A)=0,a=![]() ,b=2,求△ABC的面积S
,b=2,求△ABC的面积S
查看答案和解析>>
科目: 来源:浙江省瑞安市十校2012届高三上学期期中联考数学文科试题 题型:044
已知函数f(x)=![]() ,x∈[0,1],
,x∈[0,1],
(Ⅰ)求f(x)的单调区间和值域;
(Ⅱ)设a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1],若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围
查看答案和解析>>
科目: 来源:浙江省瑞安市十校2012届高三上学期期中联考数学文科试题 题型:044
已知抛物线y2=4x的焦点为F,直线l过点M(4,0).
(Ⅰ)若点F到直线l的距离为![]() ,求直线l的斜率;
,求直线l的斜率;
(Ⅱ)设A,B为抛物线上两点,且AB不与x轴垂直,若线段AB的垂直平分线恰过点M,求证:线段AB中点的横坐标为定值.
查看答案和解析>>
科目: 来源:浙江省瑞安市十校2012届高三上学期期中联考数学文科试题 题型:044
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.

(Ⅰ)求证:EF∥面ABC;
(Ⅱ)求证:面ADE⊥面ACD;
(Ⅲ)求四棱锥A-BCDE的体积.
查看答案和解析>>
科目: 来源:浙江省瑞安市十校2012届高三上学期期中联考数学文科试题 题型:044
设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=1na3n+1,n=1,2……,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目: 来源:浙江省瑞安市十校2012届高三上学期期中联考数学文科试题 题型:044
已知两个向量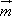 =(cos
=(cos![]() ,sin
,sin![]() ),
),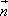 =(2
=(2![]() +sin
+sin![]() ,2
,2![]() -cos
-cos![]() ),其中
),其中![]() ∈(-
∈(-![]()
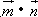 =1.
=1.
(Ⅰ)求sin(![]() +
+![]() )的值;
)的值;
(Ⅱ)求cos(![]() +
+![]()
查看答案和解析>>
科目: 来源:浙江省富阳市新登中学2012届高三上学期期中考试数学理科试题 题型:044
已知函数f(x)=![]() x3-
x3-![]() x2+(a+3)x+1,其中a为实数,且a≠0.
x2+(a+3)x+1,其中a为实数,且a≠0.
(1)若函数f(x)在x=-1处取得极值,求a的值;
(2)若不等式![]() (x)>x2-x-a+3对任意a∈(0,+∞)都成立,求实数x的取值范围.
(x)>x2-x-a+3对任意a∈(0,+∞)都成立,求实数x的取值范围.
(3)若f(x)在区间[2,4]上不单调,求实数a的取值范围.
查看答案和解析>>
科目: 来源:浙江省富阳市新登中学2012届高三上学期期中考试数学理科试题 题型:044
在数列{an}中,已知a1=-1,an+1=2an-n+1(n=1,2,3,…).
(1)证明数列{an-n}是等比数列;
(2)令bn=![]() ,Sn为数列{bn}的前n项和,求Sn的表达式;
,Sn为数列{bn}的前n项和,求Sn的表达式;
查看答案和解析>>
科目: 来源:浙江省富阳市新登中学2012届高三上学期期中考试数学理科试题 题型:044
设a∈R,函数f(x)=ax2-2x-2a.若f(x)>0解集为
A,集合B={x|1<x<3},若A∩B≠![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目: 来源:浙江省富阳市新登中学2012届高三上学期期中考试数学理科试题 题型:044
从集合M={1,2,3,4,5,6,7,8,9}中,抽取三个不同元素构成子集{a1,a2,a3}.
(Ⅰ)求对任意的i≠j,满足|ai-aj|≥2的概率;
(Ⅱ)若a1,a2,a3成等差数列,设其公差为ξ(ξ>0),求随机变量ξ的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com