已知函数f(x)＝e^ax－x，其中a≠0．

(1)若对一切x∈R，f(x)≥1恒成立，求a的取值集合．

(2)在函数f(x)的图像上取定两点A(x₁，f(x₁))，B(x₂，f(x₂))(x₁＜x₂)，记直线AB的斜率为K，问：是否存在x₀∈(x₁，x₂)，使＞k成立？若存在，求x₀的取值范围；若不存在，请说明理由．

在直角坐标系xOy中，曲线C₁的点均在C₂：(x－5)²＋y²＝9外，且对C₁上任意一点M，M到直线x＝－2的距离等于该点与圆C₂上点的距离的最小值．

(Ⅰ)求曲线C₁的方程；

(Ⅱ)设P(x₀，y₀)(y₀≠±3)为圆C₂外一点，过P作圆C₂的两条切线，分别与曲线C₁相交于点A，B和C，D．证明：当P在直线x＝－4上运动时，四点A，B，C，D的纵坐标之积为定值．

某企业接到生产3000台某产品的A，B，C三种部件的订单，每台产品需要这三种部件的数量分别为2，2，1(单位：件)．已知每个工人每天可生产A部件6件，或B部件3件，或C部件2件．该企业计划安排200名工人分成三组分别生产这三种部件，生产B部件的人数与生产A部件的人数成正比，比例系数为k(k为正整数)．

(1)设生产A部件的人数为x，分别写出完成A，B，C三种部件生产需要的时间；

(2)假设这三种部件的生产同时开工，试确定正整数k的值，使完成订单任务的时间最短，并给出时间最短时具体的人数分组方案．

已知数列{a_n}的各项均为正数，记A(n)＝a₁＋a₂＋……＋a_n，B(n)＝a₂＋a₃＋……＋a_n+1，C(n)＝a₃＋a₄＋……＋a_n+2，n＝1，2，……

(1)若a₁＝1，a₂＝5，且对任意n∈N﹡，三个数A(n)，B(n)，C(n)组成等差数列，求数列{a_n}的通项公式．

(2)证明：数列{a_n}是公比为q的等比数列的充分必要条件是：对任意n∈N^*，三个数A(n)，B(n)，C(n)组成公比为q的等比数列．

如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB＝4，BC＝3，AD＝5，∠DAB＝∠ABC＝90°，E是CD的中点．

(Ⅰ)证明：CD⊥平面PAE；

(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P－ABCD的体积．

某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示．

已知这100位顾客中的一次购物量超过8件的顾客占55％．

(Ⅰ)确定x，y的值，并求顾客一次购物的结算时间X的分布列与数学期望；

(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2.5分钟的概率．

(注：将频率视为概率)

已知函数f(x)＝axsinx－(a∈R)，且在[0，]上的最大值为

(1)求函数f(x)的解析式；

(2)判断函数f(x)在(0，π)内的零点个数，并加以证明．

如图，等边三角形OAB的边长为8，且其三个顶点均在抛物线E：x²＝2py(p＞0)上．

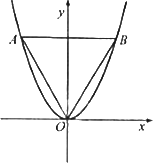
(1)求抛物线E的方程；

(2)设动直线l与抛物线E相切于点P，与直线y＝－1相较于点Q．证明以PQ为直径的圆恒过y轴上某定点．

某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数．

(1)sin²13°＋cos²17°－sin13°cos17°

(2)sin²15°＋cos²15°－sin15°cos15°

(3)sin²18°＋cos²12°－sin18°cos12°

(4)sin²(－18°)＋cos²48°－sin²(－18°)cos²48°

(5)sin²(－25°)＋cos²55°－sin²(－25°)cos²55°

(Ⅰ)试从上述五个式子中选择一个，求出这个常数

(Ⅱ)根据(Ⅰ)的计算结果，将该同学的发现推广位三角恒等式，并证明你的结论．

如图，在长方体ABCD－A₁B₁C₁D₁中，AB＝AD＝1，AA₁＝2，M为棱DD₁上的一点．

(1)求三棱锥A－MCC₁的体积；

(2)当A₁M＋MC取得最小值时，求证：B₁M⊥平面MAC．