受轿车在保修期内维修费等因素的影响，企业产生每辆轿车的利润与该轿车首次出现故障的时间有关，某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年，现从该厂已售出的两种品牌轿车中随机抽取50辆，统计书数据如下：

将频率视为概率，解答下列问题：

(Ⅰ)从该厂生产的甲品牌轿车中随机抽取一辆，求首次出现故障发生在保修期内的概率；

(Ⅱ)若该厂生产的轿车均能售出，记住生产一辆甲品牌轿车的利润为X₁，生产一辆乙品牌轿车的利润为X₂，分别求X₁，X₂的分布列；

(Ⅲ)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌轿车，若从经济效益的角度考虑，你认为应该产生哪种品牌的轿车？说明理由．

若函数h(x)满足

(1)h(0)＝1，h(1)＝0；

(2)对任意a∈[0，1]，有h(h(a))＝a；

(3)在(0，1)上单调递减．

则称h(x)为补函数．已知函数h(x)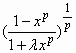＝(λ＞－1，p＞0)

(1)判函数h(x)是否为补函数，并证明你的结论；

(2)若存在ｍ∈[0，1]，使得h(m)＝m，若m是函数h(x)的中介元，记p＝(n∈N₊)时h(x)的中介元为x_n，且S_n＝，若对任意的n∈N₊，都有S_n＜，求λ的取值范围；

(3)当λ＝0，x∈(0，1)时，函数y＝h(x)的图像总在直线y＝1－x的上方，求P的取值范围．

已知三点O(0，0)，A(－2，1)，B(2，1)，曲线C上任意一点M(x，y)满足＋＝·(＋)＋2．

(1)求曲线C的方程；

(2)动点Q(x₀，y₀)(－2＜x₀＜2)在曲线C上，曲线C在点Q处的切线为l向：是否存在定点P(0，t)(t＜0)，使得l与PA，PB都不相交，交点分别为D，E，且△QAB与△PDE的面积之比是常数？若存在，求t的值．若不存在，说明理由．

在三棱柱ABC－A₁B₁C₁中，已知AB＝AC＝AA₁＝，BC＝4，在A₁在底面ABC的投影是线段BC的中点O．

(1)证明在侧棱AA₁上存在一点E，使得OE⊥平面BB₁C₁C，并求出AE的长；

(2)求平面A1B1C与平面BB₁C₁C夹角的余弦值．

如图，从A₁(1，0，0)，A₂(2，0，0)，B₁(0，2，0)，B₂(0，2，0)，C₁(0，0，1)，C₂(0，0，2)这6个点中随机选取3个点，将这3个点及原点O两两相连构成一个“立体”，记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内，此时“立体”的体积V＝0)．

(1)求V＝0的概率；

(2)求V的分布列及数学期望．

在△ABC中，角A，B，C的对边分别为a，b，c．已知A＝，bsin(＋C)－csin(＋B)＝a．

(1)求证：B－C＝

(2)若a＝，求△ABC的面积．

已知数列{a_n}的前n项和S_n＝－n²＋kn(其中k∈N)，且S_n的最大值为8．

(1)确定常数k，求a_n；

(2)求数列{}的前n项和T_n．

(Ⅰ)已知函数f(x)＝rx－x^r＋(1－r)(x＞0)，其中r为有理数，且0＜r＜1．求f(x)的最小值；

(Ⅱ)试用(Ⅰ)的结果证明如下命题：

设a₁≥0，a₂≥0，b₁，b₂为正有理数．若b₁＋b₂＝1，则≤a₂b₂；

(Ⅲ)请将(Ⅱ)中的命题推广到一般形式，并用数学归纳法证明你所推广的命题．

注：当a为正有理数时，有求导公式＝ax^a－1．

设A是单位圆x²＋y²＝1上的任意一点，l是过点A与x轴垂直的直线，D是直线l与x轴的交点，点M在直线l上，且满足|DM|＝m|DA|(m＞0，且m≠1)．当点A在圆上运动时，记点M的轨迹为曲线C．

(Ⅰ)求曲线C的方程，判断曲线C为何种圆锥曲线，并求其焦点坐标；

(Ⅱ)过原点且斜率为k的直线交曲线C于P，Q两点，其中P在第一象限，它在y轴上的射影为点N，直线QN交曲线C于另一点H．是否存在m，使得对任意的k＞0，都有PQ⊥PH？若存在，求m的值；若不存在，请说明理由．

根据以往的经验，某工程施工期间的降水量X(单位：mm)对工期的影响如下表：

历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0.3，0.7，0.9．求：

(Ⅰ)工期延误天数Y的均值与方差；

(Ⅱ)在降水量X至少是300的条件下，工期延误不超过6天的概率．