在△ABC中，内角A，B，C的对边分别为a，b，c，已知＝，

(Ⅰ)求的值；

(Ⅱ)若cosB＝，b＝2，求△ABC的面积S．

在数1和100之间插入n个实数，使得这n＋2个数构成递增的等比数列，将这n＋2个数的乘积记作T_n，再令a_n＝lgT_n，n≥1．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)设b_n＝tana_n·tana_n+1，求数列{b_n}的前n项和S_n．

某地最近十年粮食需求量逐年上升，下表是部分统计数据：

(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程y＝bx＋a；

(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量．

温馨提示：答题前请仔细阅读卷首所给的计算公式及说明．

如图，ABEDFC为多面体，平面ABED与平面ACFD垂直，点O在线段AD上，OA＝1，OD＝2，△OAB，△OAC，△ODF都是正三角形．

(Ⅰ)证明直线BC∥EF；

(Ⅱ)求棱锥F－OBED的体积．

设f(x)＝，其中a为正实数．

(Ⅰ)当a＝时，求f(x)的极值点；

(Ⅱ)若f(x)为R上的单调函数，求a的取值范围．

设直线l₁：y＝k₁x＋1，l₂：y＝k₂x－1，其中实数k₁，k₂满足k₁k₂＋2＝0，

(Ⅰ)证明l₁与l₂相交；

(Ⅱ)证明l₁与l₂的交点在椭圆2x²＋y²＝1上．

在△ABC中，a，b，c分别为内角A，B，C所对的边长，a＝，b＝，1＋2cos(B＋C)＝0，求边BC上的高．

已知函数f(x)＝x³，g(x)＝x＋．

(Ⅰ)求函数h(x)＝f(x)－g(x)的零点个数．并说明理由；

(Ⅱ)设数列{a_n}(n∈Nⁿ)满足a₁＝0(a＞0)，f(a_n+1)＝g(a_n)，证明：存在常熟M，使得对于任意的n∈Nⁿ，都有a_n≤M．

如图，椭圆C₁：＋＝1(a＞b＞0)的离心率为，x轴被曲线C₂：y＝x²－b截得的线段长等于C₁的长半轴长．

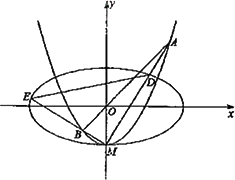
(Ⅰ)求C₁，C₂的方程；

(Ⅱ)设C₂与y轴的焦点为M，过坐标原点O的直线l与C₂相交于点A，B，直线MA，MB分别与C₁相交与D，E．

(i)证明：MD⊥ME；

(ii)记△MAB，△MDE的面积分别是S₁，S₂．问：是否存在直线l，使得＝？

请说明理由．

如图，长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动，速度为v(v＞0)，雨速沿E移动方向的分速度为e(e∈R)．E移动时单位时间内的淋雨量包括两部分：(1)P或P的平行面(只有一个面淋雨)的淋雨量，假设其值与|v－c|×S成正比，比例系数为；(2)其它面的淋雨量之和，其值为，记y为E移动过程中的总淋雨量，当移动距离d＝100，面积S＝时．

(Ⅰ)写出y的表达式

(Ⅱ)设0＜v≤10，0＜c≤5，试根据c的不同取值范围，确定移动速度v，使总淋雨量y最少．