已知函数，f₂(x)＝()^|x－m|其中m∈R且m≠0．

(Ⅰ)讨论函数f₁(x)的单调性；

(Ⅱ)若m＜－2，求函数f(x)＝f₁(x)＋f₂(x)(x∈[－2，2])的最值；

(Ⅲ)设函数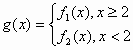当x≥2时，若对于任意的x₁∈[2，＋∞)，总存在唯一的x₂∈(－∞，2)，使得g(x₁)＝g(x₂)成立．试求m的取值范围．

如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室．已知已有两面墙的夹角为60°(即∠C＝60°)，第三面围墙的长度为6米，即AB＝6米，(两面墙的长均大于6米)．为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大．记∠ABC＝，问当为多少时，所建造的三角形露天活动室的面积最大？

设数列{a_n}的前项n和为，已知a₁＝1，S_n+1＝2S_n＋n＋1(n∈N^*)，

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若，数列{b_n}的前项和为T_n，n∈N^*证明：T_n＜2．

已知向量；令f(x)＝(＋)²，

(1)求f(x)解析式及单调递增区间；

(2)若，求函数f(x)的最大值和最小值；

(3)若f(x)＝，求sin(x－)的值．

已知{a_n}为等差数列，且a₃＝－6，a₆＝0．

(Ⅰ)求{a_n}的通项公式及前n项和S_n的最小值；

(Ⅱ)若等比数列{b_n}满足b₁＝－8，b₂＝a₁＋a₂＋a₃，求{b_n}的前n项和公式．

已知函数(a是常数)，

(Ⅰ)讨论f(x)的单调区间；

(Ⅱ)当a＝1时，方程f(x)＝m在上有两解，求m的取值范围；(e≈2.71828)

(Ⅲ)求证：ln＞(n＞1，且n∈N^*)．

已知函数f(x)＝x³＋ax²－bx＋1，(x∈R，a，b为实数)

(Ⅰ)若x＝1是函数f(x)的零点，求证：函数f(x)不是单调函数；

(Ⅱ)若函数f(x)在区间[－1，2]上是单调减函数，求a＋b的最小值．

下图是某简谐运动的一段图像，它的函数模型是f(x)＝Asin(ωx＋φ)(x≥0)，其中A＞0，ω＞0，．

(Ⅰ)根据图像求函数y＝f(x)的解析式；

(Ⅱ)将函数y＝f(x)图像上各点的横坐标缩短到原来的倍，纵坐标不变，得到函数y＝g(x)的图像，求函数y＝g(x)在上的最大值和最小值．

定义函数f_n(x)＝(1＋x)ⁿ－1，x＞－2，n∈N^*．

(1)求证：f_n(x)≥nx；

(2)是否存在区间[a，0](a＜0)，使函数h(x)＝f₃(x)－f₂(x)在区间[a，0]上的值域为[ka，0]?若存在，求出最小的k值及相应的区间[a，0]，若不存在，说明理由．

某企业投入81万元经销某产品，经销时间共60个月，市场调研表明，该企业在经销这个产品期间第X个月的利润f(x)＝(单位：万元)．为了获得更多的利润，企业将每月获得的利润再投人到次月的经营中．记第x个月的利润率为g(x)＝，例如g(3)＝

(1)求g(x)

(2)求第x个月的当月利润率；

(3)求该企业经销此产品期间，哪一个月的当月利润率最大，并求出该月的当月利润率．