定义在R上的单调函数y＝f(x)满足f(2)＝3，且对任意x，y∈R都有f(x＋y)＝f(x)＋f(y)．

(Ⅰ)试求f(0)的值并证明函数y＝f(x)为奇函数；

(Ⅱ)若f(m·3^x)＋f(3^x－9^x)＜3对任意x∈R恒成立，求实数m的取值范围．

已知集合A＝{x|(x－2)(x―2a―5)＜0}，函数的定义域为集合B．

(Ⅰ)若a＝4，求集合A∩B；

(Ⅱ)已知是“x∈B”的必要条件，求实数a的取值范围．

函数f(x)＝e^x＋2x²－3x．

(1)求证函数f(x)在区间[0，1]上存在唯一的极值点，并用二分法求函数取得极值时相应x的近似值(误差不超过0.2)；(参考数据e≈2.7，≈1.6，e^0.3≈1.3)

(2)当x≥时，若关于x的不等式f(x)≥x²＋(a－3)x＋1恒成立，试求实数a的取值范围．

如图，圆柱的高为2，底面半径为3，AE、DF是圆柱的两条母线，B、C是下底面圆周上的两点，已知四边形ABCD是正方形．

(1)求证：BC⊥BE；

(2)求正方形ABCD的边长；

(3)求直线EF与平面ABF所成角的正弦值．

函数f(x)＝ax²＋2x＋1，g(x)＝lnx．

(Ⅰ)设F(x)＝f(x)－g(x)，求F(x)的两个极值点的充要条件．

(Ⅱ)求证：当a≥0时，不等式f(x)≥g(x)恒成立．

已知函数有极值．

(Ⅰ)求c的取值范围；

(Ⅱ)若f(x)在x＝2处取得极值，且当x＜0时，f(x)＜d²＋2d恒成立，求d的取值范围．

设二次函数f(x)＝mx²＋nx＋t的图像过原点，g(x)＝ax³＋bx－3(x＞0)，f(x)，g(x)的导函数为，且，f(1)＝g(1)，．

(1)求函数f(x)，g(x)的解析式；

(2)求F(x)＝f(x)－g(x)的极小值；

(3)是否存在实常数k和m，使得f(x)≥kx＋m和g(x)≤kx＋m？若存在，求出k和m的值；若不存在，说明理由．

据调查，湖南某地区有100万从事传统农业的农民，人均年收入3000元．为了增加农民的收入，当地政府积极引资建立各种加工企业，对当地的农产品进行深加工，同时吸收当地部分农民进入加工企业工作．据估计，如果有x(x＞0)万人进入企业工作，那么剩下从事传统农业的农民的人均年收入有望提高2x％，而进入企业工作的农民人均年收入为3000a元(a＞0为常数)．

(Ⅰ)在建立加工企业后，要使该地区从事传统农业的农民的年总收入不低于加工企业建立前的年总收入，求x的取值范围；

(Ⅱ)在(Ⅰ)的条件下，当地政府应安排多少万农民进入加工企业工作，才能使这100万农民的人均年收入达到最大？

如图所示，已知ABCD－A₁B₁C₁D₁是底面为正方形的长方体，∠AD₁A₁＝60°，AD₁＝4，点P是AD₁上的动点．

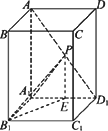
(1)当P为AD₁的中点时，求异面直线AA₁与B₁P所成角的余弦值；

(2)求PB₁与平面AA₁D₁所成角的正切值的最大值．

设函数f(x)＝ka^x－a^－x，(a＞0，a≠1)是定义在R上的奇函数

(1)求k的值，并判断函数f(x)的单调性；

(2)若f(1)＞0，解不等式f(x²＋2x)＋f(x－4)＞0；

(3)若，且g(x)＝a^2x＋a^－2x－2mf(x)在[1，＋∞)上的最小值为－2，求m的值．