已知函数在[1，＋∞)上为增函数，且∈(0，π)，f(x)＝mx－－lnx，m∈R．

(1)求的值；

(2)若f(x)－g(x)在[1，＋∞)上为单调函数，求m的取值范围；

(3)设h(x)＝，若在[1，e]上至少存在一个x₀，使得f(x₀)－g(x₀)＞h(x₀)成立，求m的取值范围．

如图示，已知平行四边形ABCD和矩形ACEF所在平面互相垂直，AB＝1，AD＝2，∠ADC＝60°，AF＝1，M是线段EF的中点．

(1)求证：AC⊥BF；

(2)设二面角A－FD－B的大小为，求sin的值；

(3)设点P为一动点，若点P从M出发，沿棱按照M→E→C的路线运动到点C，求这一过程中形成的三棱锥P－BFD的体积的最小值．

在数列{a_n}中，已知a₁＝p＞0，且a_n+1·a_n＝n²＋3n＋2，n∈N^*．

(1)若数列{a_n}为等差数列，求p的值；

(2)求数列{a_n}的通项公式；

某市某房地产公司售楼部，对最近100位采用分期付款的购房者进行统计，统计结果如下表所示：

已知分3期付款的频率为0.2，售楼部销售一套某户型的住房，顾客分1期付款，其利润为10万元；分2期、3期付款其利润都为15万元；分4期、5期付款其利润都为20万元，用η表示销售一套该户型住房的利润．

(1)求上表中a，b的值；

(2)若以频率分为概率，求事件A：“购买该户型住房的3位顾客中，至多有1位采用分3期付款”的概率P(A)；

(3)若以频率作为概率，求η的分布列及数学期望Eη．

已知向量＝(2cos²x，)，＝(1，sin2x)，函数f(x)＝·，g(x)＝．

(Ⅰ)求函数g(x)的最小正周期；

(Ⅱ)在△ABC中，a，b，c分别是角A，B，C的对边，R为△ABC外接圆的半径，且f(C)＝3，c＝1，，且a＞b，求a，b的值．

在平面直角坐标系中，已知焦距为4的椭圆的左、右顶点分别为A、B，椭圆C的右焦点为F，过F作一条垂直于x轴的直线与椭圆相交于R、S，若线段RS的长为．

(1)求椭圆C的方程；

(2)设Q(t，m)是直线x＝9上的点，直线QA、QB与椭圆C分别交于点M、N，求证：直线MN必过x轴上的一定点，并求出此定点的坐标；

已知定义在R上的函数f(x)＝ax³－3x²，其中a为大于零的常数．

(Ⅰ)当a＝时，令h(x)＝(x)＋6x，求证：当x∈(0，＋∞)时，h(x)≥2elnx(e为自然对数的底数)；

(Ⅱ)若函数g(x)＝f(x)＋(x)，x∈[0，2]，在x＝0处取得最大值，求a的取值范围

已知函数f(x)＝(x≠0)各项均为正数的数列{a_n}中a₁＝1，＝f(a_n)，(n∈N^*)．

(1)求数列{a_n}的通项公式；

(2)在数列{b_n}中，对任意的正整数n，b_n·都成立，设S_n为数列{b_n}的前n项和试比较S_n与的大小．

下面一组图形为三棱锥P－ABC的底面与三个侧面．已知AB⊥BC，PA⊥AB，PA⊥AC．

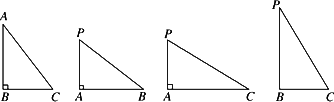
(1)在三棱锥P－ABC中，求证：平面ABC⊥平面PAB；

(2)在三棱锥P－ABC中，M是PA的中点，且PA＝BC＝3，AB＝4，求三棱锥P－MBC的体积．

近年来，我国机动车拥有量呈现快速增加的趋势，可与之配套的基础设施建设速度相对迟缓，交通拥堵问题已经成为制约城市发展的重要因素，为了解某市的交通状况，现对其6条道路进行评估，得分分别为5、6、7、8、9、10规定评估的平均得分与全市的总体交通状况等级如下表：

(1)求本次评估的平均得分，并参照上表估计该市的总体交通状况等级．

(2)用简单随机抽样方法从6条道路中抽取2条，它们的得分组成一个样本，求该样本的平均数与总体的平均数之差的绝对值不超过0.5的概率．