如图，正三棱柱ABC－A₁B₁C₁中，AB＝2，AA₁＝3，D为C₁B的中点，P为AB边上的动点．

(Ⅰ)若P为AB中点，求证DP∥平面ACC₁A₁；

(Ⅱ)若AP＝3PB，求三棱锥B－CDP的体积．

如图，曲线C₁是以原点O为中心，F₁、F₂为焦点的椭圆的一部分，曲线C₂是以原点O为顶点，F₂为焦点的抛物线的一部分，是曲线C₁和C₂的交点．

(Ⅰ)求曲线C₁和C₂所在的椭圆和抛物线的方程；

(Ⅱ)过F₂作一条与x轴不垂直的直线，分别与曲线C₁、C₂依次交于B、C、D、E四点，若G为CD中点，H为BE中点，问是否为定值，若是，求出定值；若不是，请说明理由．

已知函数f(x)＝lnx－ax－3(a≠0)．

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若对于任意的a∈[1，2]，函数g(x)＝x³＋[m－2(x)]在区间(a，3)上有最值，求实数m的取值范围．

已知数列{b_n}是等差数列，b₁＝1，b₁＋b₂＋b₃＋…＋b₁₀＝100．

(Ⅰ)求数列{b_n}的通项公式；

(Ⅱ)设数列{a_n}的通项记T_n是数列{a_n}的前n项之积，即T_n＝b₁·b₂·b₃…b_n，试证明：

如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘，转盘停止转动时，箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动)，且箭头A指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘，得分情况记为(a，b)(假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动)．

(Ⅰ)求某个家庭得分为(5，3)的概率；

(Ⅱ)若游戏规定：一个家庭的得分为参与游戏的两人得分之和，且得分大于等于8的家庭可以获得一份奖品．求某个家庭获奖的概率；

(Ⅲ)若共有5个家庭参加家庭抽奖活动．在(Ⅱ)的条件下，记获奖的家庭数为X，求X的分布列及数学期望．

如图，四棱锥P－ABCD中，底面ABCD为平行四边形，AB＝2AD＝2，BD＝，PD⊥底面ABCD．

(1)证明：平面PBC⊥平面PBD；

(2)若二面角P－BC－D为，求AP与平面PBC所成角的正弦值．

已知向量＝(cosx，－1)，向量＝(sinx，－)，函数f(x)＝(＋)·．

(Ⅰ)求f(x)的最小正周期T；

(Ⅱ)已知a，b，c分别为△ABC内角A，B，C的对边，A为锐角，a＝1，c＝，且f(A)恰是f(x)在[0，]上的最大值，求A，b和△ABC的面积．

已知函数f(x)＝px－－2lnx，g(x)＝，

(Ⅰ)若p＝2，求曲线f(x)在点(1，f(1))处的切线方程；

(Ⅱ)若函数f(x)在其定义域内为增函数，求正实数p的取值范围；

(Ⅲ)若p²－p≥0，且至少存在一点x₀∈[1，e]，使得f(x₀)＞g(x₀)成立，求实数p的取值范围．

已知m＞1，直线l：x－my－＝0，椭圆C：＋y2＝1，F₁，F₂分别为椭圆C的左、右焦点．

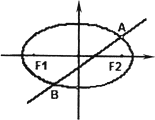
(Ⅰ)当直线l过右焦点F₂时，求直线l的方程；

(Ⅱ)设直线l与椭圆C交于A，B两点，△AF₁F₂，△BF₁F₂的重心分别为G，H．若原点O在以线段GH为直径的圆内，求实数m的取值范围．

投掷一个质地均匀的、每个面上标有一个数字的正方体玩具，它的六个面中，有两个面标的数字是0，两个面标的数字是2，两个面标的数字是4，将此玩具连续抛掷两次，以两次朝上一面出的数字分别作为点P的横坐标和纵坐标．

(Ⅰ)求点P落在区域C：x²＋y²≤10内的概率；

(Ⅱ)若以落在区域C：x²＋y²≤10上的所有点为顶点作面积最大的多边形区域M，在区域C上随机撒一粒豆子，求豆子落在区域M上的概率．