已知椭圆M的中心为坐标原点，且焦点在x轴上，若M的一个顶点恰好是抛物线y²＝8x的焦点，M的离心率，过M的右焦点F作不与坐标轴垂直的直线l，交M于A，B两点．

(1)求椭圆M的标准方程；

(2)设点N(t，0)是一个动点，且(＋)⊥，求实数t的取值范围．

哈尔滨冰雪大世界每年冬天都会吸引大批游客，现准备在景区内开设经营热饮等食品的店铺若干．根据以往对500名40岁以下(含40岁)人员和500名40岁以上人员的统计调查，有如下一系列数据：40岁以下(含40岁)人员购买热饮等食品的有260人，不购买热饮食品的有240人；40岁以上人员购买热饮等食品的有220人，不购买热饮等食品的有280人，请根据以上数据作出2×2列联表，并运用独立性检验思想，判断购买热饮等食品与年龄(按上述统计中的年龄分类方式)是否有关系？

注：要求达到99.9％的把握才能认定为有关系．

附：K²＝

已知斜三棱柱ABC－A₁B₁C₁的底面是正三角形，侧面ABB₁A₁是边长为2的菱形，且∠A₁AB＝60°，M是AB的中点，MA₁⊥AC．

(1)求证：MA₁⊥平面ABC；

(2)求点M到平面AA₁C₁C的距离．

已知{a_n}为等比数列，a₁＝1，a₄＝27．S_n为等差数列{b_n}的前n项和，b₁＝3，S₅＝35．

(1)求{a_n}和{b_n}的通项公式；

(2)设T_n＝a₁b₁＋a₂b₂＋…＋a_nb_n，求T_n．

现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向)．在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离(位移)，而是实际路程(如图)．在直角坐标平面内，我们定义A(x₁，y₁)，B(x₂，y₂)两点间的“直角距离”为：D_(AB)＝|x₁－x₂|＋|y₁－y₂|．

(1)在平面直角坐标系中，写出所有满足到原点的“直角距离”为2的“格点”的坐标．(格点指横、纵坐标均为整数的点)

(2)求到两定点F₁、F₂的“直角距离”和为定值2a(a＞0)的动点轨迹方程，并在直角坐标系内作出该动点的轨迹．

①F₁(－1，0)，F₂(1，0)，a＝2；

②F₁(－1，－1)，F₂(1，1)，a＝2；

③F₁(－1，－1)，F₂(1，1)，a＝4．

(3)写出同时满足以下两个条件的“格点”的坐标，并说明理由(格点指横、纵坐标均为整数的点)．

①到A(－1，－1)，B(1，1)两点“直角距离”相等；

②到C(－2，－2)，D(2，2)两点“直角距离”和最小．

设数列{a_n}的前n项和为S_n，且满足2a_n－S_n＝1，n∈N^*．

(1)求数列{a_n}的通项公式；

(2)在数列{a_n}的第两项之间都按照如下规则插入一些数后，构成新数列{b_n}；a_n和a_n+1两项之间插入n个数，使这n＋2个数构成等差数列，求b₂₀₁₂的值．

(3)对于(2)中的数列{b_n}，若b_m＝a_n，并求b₁＋b₂＋b₃＋…＋b_m．(用n表示)

某创业投资公司拟投资开发某种新能源产品，估计能获得10万元到1000万元的投资收益．现准备制定一个对科研课题组的奖励方案：奖金y(单位：万元)随投资收益x(单位：万元)的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20％．

(1)，若建立函数y＝f(x)模型制定奖励方案，试用数学语言表述该公司对奖励函数f(x)模型的基本要求，并分析函数是否符合公司要求的奖励函数模型，并说明原因；

(2)若该公司采用模型函数作为奖励函数模型，试确定最小的正整数a的值．

如图所示，正方体ABCD－A₁B₁C₁D₁的棱长为1，点M、N分别是面对角线A₁B和B₁D₁的中点．

(1)求证：MN⊥AB；

(2)求三棱锥N－MBC的体积．

在△ABC中，角A、B、C所对的边分别为a，b，c．设向量＝(a，cosB)，＝(b，cosA)，且∥，≠．求sinA＋sinB的取值范围．

现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向)．在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离(位移)，而是实际路程(如图)．在直角坐标平面内，我们定义A(x₁，y₁)，B(x₂，y₂)两点间的“直角距离”为：D_(AB)＝|x₁－x₂|＋|y₁－y₂|．

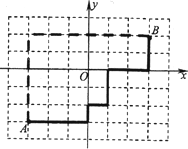
(1)已知A(－3，－3)，B(3，2)，求A、B两点的距离D_(AB)．

(2)求到定点M(1，2)的“直角距离”为2的点的轨迹方程．

并写出所有满足条件的“格点”的坐标(格点是指横、纵坐标均为整数的点)．

(3)求到两定点F₁、F₂的“直角距离”和为定值2a(a＞0)的动点轨迹方程，并在直角坐标系内作出该动点的轨迹．

①F₁(－1，0)，F₂(1，0)，a＝2；

②F₁(－1，－1)，F₂(1，1)，a＝2；

③F₁(－1，－1)，F₂(1，1)，a＝4．