某校高二年级甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名乒乓球选手，学校计划从甲、乙两班各选2名选手参加体育交流活动．

(Ⅰ)求选出的4名选手均为男选手的概率．

(Ⅱ)若b_n＝a_n·loga_n，数列{b_n}的前n项和为S_n，求使s_n＋n·2ⁿ⁺¹＞50成立的正整数n的最小值．

已知f(x)＝m·n，其中m＝(sinωx＋cosωx，cosωx)，n＝(cosωx－sinωx，2sinωx)(ω＞0)，若f(x)图象中相邻的两条对称轴间的距离不小于π．

(Ⅰ)求ω的取值范围

(Ⅱ)在△ABC中，a，b，c分别为角A，B，C的对边，．当ω取最大值时，f(A)＝1，求b，c的值．

(本小题满分14分)

设椭圆的左、右焦点分别为F1、F2，上顶点为A，离心率e＝，在x轴负半轴上有一点B，且．

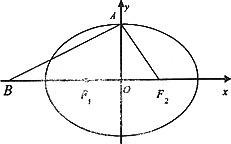
(Ⅰ)若过A、B、F₂三点的圆恰好与直线相切，求椭圆C的方程；

(Ⅱ)在(Ⅰ)的条件下，过右焦点F₂作斜率为k的直线与椭圆C交于M、N两点，在x轴上是否存在点p(m，0)，使得以PM，PN为邻边的平行四边形是菱形，如果存在，求出m的取值范围；如果不存在，说明理由．

已知函数f(x)＝ax²＋lnx(a∈R)．

(Ⅰ)当时，求f(x)在区间[1，e]上的最大值和最小值；

(Ⅱ)如果在公共定义域D上的函数g(x)，f₁(x)，f₂(x)满足f₁(x)＜g(x)＜f₂(x)，那么就称g(x)为f₁(x)、f₂(x)的“活动函数”，已知函数f₁(x)＝(a－)x²＋2ax＋(1－a²)lnx，f₂(x)＝x²＋2ax，若在区间(1，＋∞)上，函数f(x)是f₁(x)、f₂(x)的“活动函数”，求实数a的取范围．

如图所示，在正三棱柱ABC－A₁B₁C₁中，底面边长和侧棱长都是2，D是侧棱CC₁上任意一点，E是A₁B₁的中点．

(Ⅰ)求证：A₁B₁//平面ABD；

(Ⅱ)求证：AB⊥CE；

(Ⅲ)求三棱锥C－ABE的体积．

某网站体育版块足球栏目组发起了“射手的上一场进连续进球有关系”的调查活动，在所有参与调查的人中，持“有关系”“无关系”“不知道”态度的人数如表所示：

(Ⅰ)在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从持“有关系”态度的人中抽取45人，求n的值；

(Ⅱ)在持“不知道”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中任选取2人，求至少一人在40岁以下的概率；

(Ⅲ)在接受调查的人中，有8人给这项活动打出分数如下：9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2，把这8个人打出的分数看做一个总体，从中任取1个数，求该数与总体平均数之差的绝对值超过0.6的概率．

已知各项均不相等的等差数列{a_n}的前四项和S₄＝14，a₃是a₁，a₇的等比中项．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)设T_n为数列的前n项和，若对一切n∈N^*恒成立，求实数λ的最大值．

已知f(x)＝m·n，其中m＝(sinωx＋cosωx，cosωx)，n＝(cosωx－sinωx，2sinωx)(ω＞0)，若f(x)图象中相邻的两条对称轴间的距离不小于π．

(Ⅰ)求ω的取值范围；

(Ⅱ)在△ABC中，a，b，c分别为角A，B，C的对边，．当ω取最大值时，f(A)＝1，求b，c的值．

设椭圆C：的一个顶点与抛物线：x²＝4y的焦点重合，F₁、F₂分别是椭圆的左、右焦点，离心率，过椭圆右焦点F₂的直线l与椭圆C交于M、N两点．

(Ⅰ)求椭圆C的方程；

(Ⅱ)是否存在直线l，使得·＝－1，若存在，求出直线l的方程；若不存在，说明理由；

(Ⅲ)若AB是椭圆C经过原点O的弦，MN∥AB，求的值．

已知函数f(x)＝ax＋lnx(a∈R)．

(Ⅰ)求f(x)的单调区间；

(Ⅱ)设g(x)＝x²－2x＋1，若对任意x₁∈(0，＋∞)，总存在x₂∈[0，1]，使得f(x₁)＜g(x₂)，求实数a的取值范围．