如图，在直角梯形ABCP中，AB＝BC＝3，AP＝6，CD⊥AP于D，现将△PCD沿线段CD折成60°的二面角P－CD－A，设E，F，G分别是PD，PC，BC的中点．

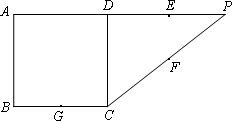
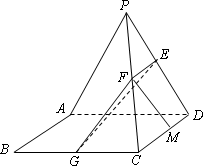
(Ⅰ)求证：PA∥平面EFG；

(Ⅱ)若M为线段CD上的动点，问点M在什么位置时，直线MF与平面EFG所成角为60°．

已知正项数列{a_n}的前n项和为S_n，且满足S_n＋a_n＝1．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)设数列{b_n}满足b_n＝(n－2)a_n，且数列{b_n}的前n项和为T_n，求证：数列{2ⁿT_n}为等差数列．

已知函数，x∈R．

(Ⅰ)当时，求f(x)的值；

(Ⅱ)已知△ABC中，角A，B，C的对边分别为a，b，c．若，b＋c＝2．求a的最小值．

如图，已知动直线l经过点P(4，0)，交抛物线y²＝2ax(a＞0)于A，B两点，坐标原点O是PQ的中点，设直线AQ，BQ的斜率分别为k₁，k₂．

(1)证明：k₁＋k₂＝0

(2)当a＝2时，是否存在垂直于x轴的直线，被以AP为直径的圆截得的弦长为定值？若存在，请求出直线的方程；若不存在，请说明理由．

已知函数f(x)＝e^x(x²＋ax－a)，其中a是常数．

(1)当a＝1时，求f(x)在点(1，f(1))处的切线方程；

(2)求f(x)在区间[0，＋∞)上的最小值．

如图，在直三棱柱ABC－A₁B₁C₁中，AC⊥BC，AC＝BC＝1，CC₁＝2，点D是AA₁的中点．

(1)证明：平面BC₁D⊥平面BCD；

(2)求CD与平面BC₁D所成角的正切值；

已知正项数列{a_n}的前项和为S_n，且满足S_n＋a_n＝1

(1)求数列{a_n}的通项公式；

(2)设，则是否存在数列{b_n}，满足b₁c₁＋b₂c₂＋…＋b_nc_n＝(2n－1)2ⁿ⁺¹＋2对一切正整数n都成立？若存在，请求出数列{b_n}的通项公式；若不存在，请说明理由．

已知向量＝与＝(1，y)共线，且有函数y＝f(x)

(Ⅰ)求函数y＝f(x)的周期与最大值；

(Ⅱ)已知锐角△ABC的三个内角分别是A、B、C，若有f(A－)＝，边BC＝，sinB＝，求AC的长．

设函数f(x)＝(2－a)lnx＋＋2ax．

(1)当a＝0时，求f(x)的极值；

(2)当a≠0时，求f(x)的单调区间；

(3)当a＝2时，对任意的正整数n，在区间上总有m＋4个数使得f(a₁)＋f(a₂)＋f(a₃)＋…＋f(a_m)＜f(a_m+1)＋f(_m+2)＋f(a_m+3)＋f(a_m+4)成立，试求正整数m的最大值．

设椭圆C：＋＝1(a＞b＞0)的离心率e＝，右焦点到直线＋＝1的距离d＝，O为坐标原点．

(Ⅰ)求椭圆C的方程；

(Ⅱ)过点O作两条互相垂直的射线，与椭圆C分别交于A，B两点，证明点O到直线AB的距离为定值，并求弦AB长度的最小值．