已知函数f(x)＝x³＋ax²－bx＋1(x∈R，a，b为实数)有极值，且在x＝1处的切线与直线x－y＋1＝0平行．

(1)求实数a的取值范围；

(2)是否存在实数a，使得函数f(x)的极小值为1，若存在，求出实数a的值；若不存在，请说明理由；

(3)设a＝，f(x)的导数为(x)，令g(x)＝－3，x∈(0，∞)

求证：gⁿ(x)－xⁿ－≥2ⁿ－2(n∈N^*)

已知过点A(0，4)的直线l与以F为焦点的抛物线C：x²＝py相切于点T(－4，y₀)；中心在坐标原点，一个焦点为F的椭圆与直线l有公共点．

(1)求直线l的方程和焦点F的坐标；

(2)求当椭圆的离心率最大时椭圆的方程；

(3)设点M(x₁，y_l)是抛物线C上任意一点，D(0，－2)为定点，是否存在垂直于y轴的直线l^/被以MD为直径的圆截得的弦长为定值？请说明理由．

某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动)．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．

(1)求合唱团学生参加活动的人均次数；

(2)从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率；

(3)从合唱团中任选两名学生，用ξ表示这两人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ．

如图，P－AD－C是直二面角，四边形ABCD是∠BAD＝120°的菱形，AB＝2，PA⊥AD，E是CD的中点，设PC与平面ABCD所成的角为45°．

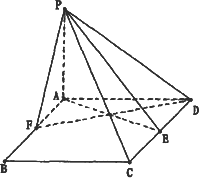
(1)求证：平面PAE⊥平面PCD；

(2)试问在线段AB(不包括端点)上是否存在一点F，使得二面角A－PE－D的大小为45°？若存在，请求出AF的长，若不存在，请说明理由．

已知函数f(x)＝2sin(ωx＋)(ω＞0，0＜＜π)的最小正周期为π，且f()＝．

(1)求ω，的值；

(2)若f()＝－(0＜α＜π)，求cos2α

已知函数f(x)＝|x－a|－lnx，(x＞0)，h(x)＝ax－1(a∈R)

(1)若a＝1，求f(x)的单调区间及f(x)的最小值；

(2)若a＞0，求f(x)的单调区间；

(3)若，求a的最小正整数值．

已知抛物线W：y＝ax²经过点A(2，1)，过A作倾斜角互补的两条不同的直线L₁，L₂．

(1)求抛物线W的方程及其准线方程；

(2)当直线L₁与抛物线W相切时，求直线L₂与抛物线W所围成封闭区域的面积；

(3)设直线L₁、L₂分别交抛物线W于B、C两点(均不与A重合)，若以BC为直径的圆与抛物线的准线相切，求直线BC的方程．

已知数列{a_n}满足：，且b_n＝a_2n－2，n∈N^*．

(1)求a₂，a₃，a₄；

(2)求证：数列{b_n}为等比数列，并求其通项公式；

(3)若S_2n+1＝a₁＋a₂＋…＋a_2n＋a_2n+1，求S_2n+1．

如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图，在直观图中，M是BD的中点，左视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．

(1)求证：EM∥平面ABC；

(2)求出该几何体的体积；

(3)试问在平面ACDE上是否存在点N，使MN⊥平面BDE？若存在，确定点N的位置；若不存在，说明理由．

围棋对局中，执黑棋者先下，执白棋者后下．一次围棋比赛中，甲乙进入最后的冠军争夺战，决赛规则是三局两胜制(即三局比赛中，谁先赢得两局，就获得冠军)，假定每局比赛没有平局，且每局比赛由裁判扔硬币决定谁执黑棋．根据甲乙双方以往对局记录，甲执黑棋对乙的胜率为，甲执白棋对乙的胜率为

(1)求乙在一局比赛中获胜的概率；

(2)若冠军获得奖金10万元，亚军获得奖金5万元，且每局比赛胜方获得奖金1万元，负方获得奖金0.5万元，记甲在决赛中获得奖金数为X万元．求X的分布列和期望EX．