已知函数f(x)＝x³－ax²－x＋2．(a∈R)．

(1)当a＝1时，求函数f(x)的极值；

(2)若对x∈R，有(x)≥|x|－成立，求实数a的取值范围．

已知椭圆的离心率为，椭圆短轴的一个端点与两个焦点构成的三角形的面积为．

(Ⅰ)求椭圆C的方程；

(Ⅱ)已知动直线y＝k(x＋1)与椭圆C相交于A、B两点．

①若线段AB中点的横坐标为，求斜率k的值；

②已知点，求证：·为定值．

一口袋中装有编号为1、2、3、4、5、6、7的七个大小相同的小球，现从口袋中一次随机抽取两球，每个球被抽到的概率是相等的，用符号(a，b)表示事件“抽到的两球的编号分别为a，b，且a＜b”．

(Ⅰ)总共有多少个基本事件？用列举法全部列举出来；

(Ⅱ)求所抽取的两个球的编号之和大于6且小于10的概率．

如图(1)，△ABC是等腰直角三角形，AC＝BC＝4，E、F分别为AC、AB的中点，将△AEF沿EF折起，使A₁在平面BCEF上的射影O恰好为EC的中点，得到图(2)．

(Ⅰ)求证：EF⊥A₁C；

(Ⅱ)求三棱锥F－A₁BC的体积．

已知数列{a_n}满足：S_n＝1－a_n(n∈N^*)，其中S_n为数列{a_n}的前n项和．

(Ⅰ)试求{a_n}的通项公式；

(Ⅱ)若数列{b_n}满足：b_n＝(n∈N^*)，试求{b_n}的前n项和公式T_n．

选修4－5：不等式选讲

设函数f(x)＝|x－1|＋|x－a|．

(Ⅰ)若a＝－1，解不等式f(x)≥3；

(Ⅱ)如果关于x的不等式f(x)≤2有解，求a的取值范围．

选修4－4：坐标系与参数方程

已知直线的极坐标方程为ρsin(＋)＝，圆M的参数方程为 (其中为参数)．

(Ⅰ)将直线的极坐标方程化为直角坐标方程；

(Ⅱ)求圆M上的点到直线的距离的最小值．

选修4－1几何证明选讲

如图，在Rt△ABC中，∠C＝90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．

(1)求证：AC是△BDE的外接圆的切线；

(2)若AD＝2，AE＝6，求EC的长．

已知函数f(x)＝x－ax²－ln(1＋x)，其中a∈R．

(Ⅰ)若x＝2是f(x)的极值点，求a的值；

(Ⅱ)求f(x)的单调区间；

(Ⅲ)若f(x)在[0，＋∞)上的最大值是0，求a的取值范围．

如图，已知椭圆的离心率为，以该椭圆上的点和椭圆的左、右焦点F₁，F₂为顶点的三角形的周长为4(＋1)．一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任一点，直线PF₁和PF₂与椭圆的交点分别为A、B和C、D．

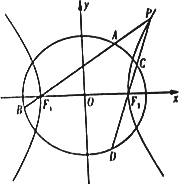
(Ⅰ)求椭圆和双曲线的标准方程；

(Ⅱ)设直线PF₁、PF₂的斜率分别为k₁、k₂，证明k₁·k₂＝1；

(Ⅲ)是否存在常数λ，使得|AB|＋|CD|＝λ|AB|·|CD|恒成立？若存在，求λ的值；若不存在，请说明理由．