在△ABC中，角A，B，C所对的边分别为a，b，c，且asinB－bcosC＝ccosB．

(Ⅰ)判断△ABC的形状；

(Ⅱ)若f(x)＝sinx＋cosx，求f(A)的最大值．

已知函数f(x)＝x²＋x．，(x)为函数f(x)的导函数．

(1)若数列{a_n}满足a_n+1＝(a_n)，且a₁＝1，求数列{a_n}的通项公式；

(2)若数列{b_n}满足b₁＝b，b_n+1＝f(b_n)．

(i)是否存在实数b，使得数列{b_n}是等差数列？若存在，求出b的值；若不存在，请说明理由．

(ii)若b＞0，求证：

已知椭圆的离心率为，且经过点M(－2，0)．

(Ⅰ)求椭圆C的标准方程；

(Ⅱ)设直线l：y＝kx＋m与椭圆C相交于A(x₁，y₁)，B(x₂，y₂)两点，连接MA，MB并延长交直线x＝4于P，Q两点，设y_P，y_Q分别为点P，Q的纵坐标，且，求证直线l过定点．

已知函数f(x)＝ax²－(a＋2)x＋lnx．

(Ⅰ)当a＝1时，求曲线y＝f(x)在点(1，f(1))处的切线方程；

(Ⅱ)当a＞0时，若f(x)在区间[1，e]上的最小值为－2，求a的取值范围；

(Ⅲ)若对任意x₁，x₂∈(0，＋∞)，x₁＜x₂，且f(x₁)＋2x₁＜f(x₂)＋2x₂恒成立，求a的取值范围．

某班共有学生40人，将一次数学考试成绩(单位：分)绘制成频率分布直方图，如图所示．

(Ⅰ)请根据图中所给数据，求出a的值；

(Ⅱ)从成绩在[50，70)内的学生中随机选3名学生，求这3名学生的成绩都在[60，70)内的概率；

(Ⅲ)为了了解学生本次考试的失分情况，从成绩在[50，70)内的学生中随机选取3人的成绩进行分析，用X表示所选学生成绩在[60，70)内的人数，求X的分布列和数学期望．

四棱锥P－ABCD中，底面ABCD是边长为2的菱形，侧面PAD⊥底面ABCD，∠BCD＝60°，PA＝PD＝，E是BC的中点，点Q在侧棱PC上．

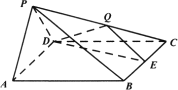
(Ⅰ)求证：AD⊥PB；

(Ⅱ)若Q是PC的中点，求二面角E－DQ－C的余弦值；

(Ⅲ)若，当PA//平面DEQ时，求A的值．

在△ABC中，角A，B，C所对的边分别为a，b，c，且asinB－bcosC＝ccosB．

(Ⅰ)判断△ABC的形状；

(Ⅱ)若，求f(A)的取值范围．

已知各项均为非负整数的数列A₀∶a₀，a₁，…，a_n(n∈N^*)，满足a₀＝0，a₁＋…＋a_n＝n．若存在最小的正整数k，使得a_k＝k(k≥1)，则可定义变换T，变换T将数列A₀变为T(A₀)∶a₀＋1，a₁＋1，…，a_k－1＋1，0，a_k+1，…，a_n．设A_i+1＝T(A_i)，i＝0，1，2…．

(Ⅰ)若数列A₀：0，1，1，3，0，0，试写出数列A₅；若数列A₄：4，0，0，0，0，试写出数列A₀；

(Ⅱ)证明存在数列A₀，经过有限次T变换，可将数列A₀变为数列；

(Ⅲ)若数列A₀经过有限次T变换，可变为数列．设S_m＝a_m＋a_m+1＋…＋a_n，m＝1，2，…，n，求证a_m＝S_m－[](m＋1)，其中[]表示不超过的最大整数．

已知椭圆C：＋＝1(a＞b＞0)的两个焦点分别为F₁(－，0)，F₂(，0)，点M(1，0)与椭圆短轴的两个端点的连线相互垂直．

(Ⅰ)求椭圆C的方程；

(Ⅱ)过点M(1，0)的直线l与椭圆C相交于A，B两点，设点N(3，2)，记直线AN，BN的斜率分别为k₁，k_2，求证：k₁＋k₂为定值．

已知函数f(x)＝(ax²－1)·ex，a∈R．

(Ⅰ)若函数f(x)在x＝1时取得极值，求a的值；

(Ⅱ)当a≤0时，求函数f(x)的单调区间．