已知对于任意非零实数m，不等式|4m－1|＋|1－m|≥|m|(|2x－3|－|x－1|)恒成立，求实数x的取值范围．

在平面直角坐标系xOy中，曲线C₁的参数方程为为参数)．在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C₁：的极坐标方程为P＝6coscp．射线l的极坐标方程为＝α，l与C₁的交点为A，l与C₂除极点外一个交点为B．当α＝0时，|AB|＝4．

(Ⅰ)求C₁，C₂直角坐标方程；

(Ⅱ)设C₁与y轴正半轴交点为D，当时，求直线BD的参数方程．

如图所示，已知⊙O₁和⊙O₂相交于A、B两点，过A点作⊙O₁的切线交⊙O₂于点C，过点B作两圆的割线，分别交⊙O₁、⊙O₂于点D、E，DE与AC相交于点P．

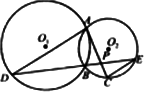
(Ⅰ)求证：AD∥EC；

(Ⅱ)若AD是⊙O₂的切线，且PA＝6，PC＝2，BD＝9，求AD的长．

已知函数

(Ⅰ)求f(x)的极值；

(Ⅱ)若x₁∈(0，＋∞)，x₂∈[1，2]使lnx₁＞x₁x－ax₁x₂成立，求a的取值范围；

(Ⅲ)已知x₁＞0，x₂＞0，且x₁＋x₂＜e，求证：(x₁＋x₂)^x₁^x₂＞(x₁x₂)^x₁^+x₂．

已知椭圆，F₁、F₂分别为椭圆C的左、右焦点，P为椭圆C上一点(不是顶点)，△PF₁F₂内一点G满足3＝＋，其中＝(a，a)．

(Ⅰ)求椭圆C的离心率；

(Ⅱ)若椭圆C短轴长为，过焦点F₂的直线l与椭圆C相交于A、B两点(A、B不是左右顶点)，求△F₁AB面积的最大值．

如图，在三棱锥P－ABC中，PB⊥平面ABC，△ABC是直角三角形，∠ABC，＝90°，AB＝BC＝2，∠PAB＝45°，点D、E、F分别为AC、AB、BC的中点．

(Ⅰ)求证：EF⊥PD；

(Ⅱ)求三棱锥D－PEF的体积；

(Ⅲ)求二面角E－PF－B的正切值．

上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．某部门从参加创作的507名画师中随机抽出100名画师，测得画师年龄情况如下表所示，

(Ⅰ)在频率分布表中的①、②位置分别应填数据为________、________；在答题卡的图中补全频率分布直方图；

(Ⅱ)根据频率分布直方图估计这507名画师中年龄在[30，35)岁的人数(结果取整数)；

(Ⅲ)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动，其中选取2名画师担任解说员工作，记这2名画师中“年龄低于30岁”的人数为ξ，求ξ的分布列及数学期望．

已知a＞0，函数(其中e为自然对数的底数)．

(Ⅰ)求函数f(x)在区间(0，e]上的最小值；

(Ⅱ)设数列{a_n}的通项，S_n是前n项和，证明：S_n－1＜lnn(n≥2)．

设动点P(x，y)(x≥0)到定点的距离比到y轴的距离大．记点P的轨迹为曲线C．

(Ⅰ)求点P的轨迹方程；

(Ⅱ)设圆M过A(1，0)，且圆心M在P的轨迹上，BD是圆M在y轴的截得的弦，当M运动时弦长BD是否为定值？说明理由；

(Ⅲ)过作互相垂直的两直线交曲线C于G、H、R、S，求四边形面GRHS的最小值．

如图，在四棱锥S－ABCD中，底面ABCD为平行四边形，SA⊥底面ABCD，AB＝2，AD＝1，SB＝，∠BAD＝120°，E在棱SD上，

(Ⅰ)当SE＝3ED时，求证：SD⊥平面AEC；

(Ⅱ)当二面角S－AC－E的大小为30°时，求直线AE与平面CDE所成角的正弦值．