如图，三棱锥A－BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形．

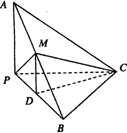
(1)求证：DM∥平面APC；

(2)求证：平面ABC⊥平面APC；

(3)若BC＝4，AB＝20，求三棱锥D－BCM的体积．

设函数f(x)＝ax＋(x－1)，若a是从1，2，3三个数中任取一个数，b是从2，3，4，5四个数中任取一个数，求f(x)＞b恒成立的概率．

△ABC的三个内角A，B，C所对的边分别为a，b，c，向量＝(－1，1)，＝(cosBcosC，sinBsinC－)，且⊥．

(1)求A的大小；

(2)现在给出下列三个条件：①a＝1；②2c－(＋1)b＝0；③B＝45°，试从中选择两个条件以确定△ABC，求出所确定的△ABC的面积．(注：只需要选择一种方案答题，如果用多种方案答题，则按第一方案给分)．

在极坐标系中，O为极点，半径为2的圆C的圆心的极坐标为(2，)．

(1)求圆C的极坐标方程；

(2)P是圆C上一动点，点Q满足3＝，以极点O为原点，以极轴为x轴正半轴建立直角坐标系，求点Q的轨迹的直角坐标方程．

如图，AB、CD是圆的两条平行弦，BE∥AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC＝ED＝1，PA＝2．

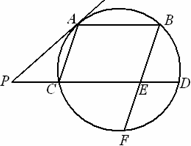
(Ⅰ)求AC的长；

(Ⅱ)求证：BE＝EF．

设函数．

(Ⅰ)求f(x)的单调区间和极值；

(Ⅱ)是否存在实数a，使得关于x的不等式f(x)≥0的解集为(0，＋∞)？若存在，求a的取值范围；若不存在，试说明理由．

设椭圆E：(a，b＞0)过M(2，)，N(，1)两点，O为坐标原点，

(Ⅰ)求椭圆E的方程；

(Ⅱ)是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A，B，且⊥？若存在，写出该圆的方程，并求|AB|的取值范围，若不存在说明理由．

如图，在底面为直角梯形的四棱锥P－ABCD中AD∥BC，∠ABC＝90°，PD⊥平面ABCD，AD＝1，AB＝，BC＝4．

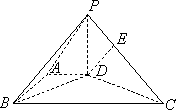
(1)求证：BD⊥PC；

(2)求直线AB与平面PDC所成的角；

(3)设点E在棱PC上，＝λ，若DE∥平面PAB，求λ的值．

符合下列三个条件之一，某名牌大学就可录取：

①获国家高中数学联赛一等奖(保送录取，联赛一等奖从省高中数学竞赛优胜者中考试选拔)；

②自主招生考试通过并且高考分数达到一本分数线(只有省高中数学竞赛优胜者才具备自主招生考试资格)；

③高考分数达到该大学录取分数线(该大学录取分数线高于一本分数线)．

某高中一名高二数学尖子生准备报考该大学，他计划：若获国家高中数学联赛一等奖，则保送录取；若未被保送录取，则再按条件②、条件③的顺序依次参加考试．

已知这名同学获省高中数学竞赛优胜奖的概率是0.9，通过联赛一等奖选拔考试的概率是0.5，通过自主招生考试的概率是0.8，高考分数达到一本分数线的概率是0.6，高考分数达到该大学录取分数线的概率是0.3.

(Ⅰ)求这名同学参加考试次数ξ的分布列及数学期望；

(Ⅱ)求这名同学被该大学录取的概率．

对于给定数列{a_n}，如果存在实常数p，q，使得a_n+1＝pa_n＋q对于任意n∈N^*都成立，我们称数列{a_n}是“M类数列”．

(Ⅰ)已知数列{b_n}是“M类数列”且b_n＝2n，求它对应的实常数p，q的值；

(Ⅱ)若数列{c_n}满足c₁＝1，c_n+1－c_n＝2ⁿ(n∈N^*)，求数列{c_n}的通项公式．并判断{c_n}是否为“M类数列”，说明理由．