设函数f(x)＝lnx－ax，g(x)＝e^x－ax，其中a为实数．

(1)若f(x)在(1，＋∞)上是单调减函数，且g(x)在(1，＋∞)上有最小值，求a的范围；

(2)若g(x)在(－1＋∞)上是单调增函数，试求f(x)的零点个数，并证明你的结论．

设{a_n}是首项为a，公差为d的等差数列(d≠0)，S_n是其前n项和．记，n∈N^*，其中c为实数．

(1)若c＝0，且b₁，b₂，b₄成等比数列，证明：S_nk＝n²S_k(k，n∈N^*)；

(2)若{b_n}是等差数列，证明：c＝0．

如图，游客从某旅游景区的景点处下山至C处有两种路径．一种是从沿A直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．

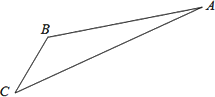
现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50 m/min．在甲出发2 min后，乙从A乘缆车到B，在B处停留1 min后，再从B匀速步行到C．假设缆车匀速直线运动的速度为130 m/min，山路AC长为1260 m，经测量，，．

(1)求索道AB的长；

(2)问乙出发多少分钟后，乙在缆车上与甲的距离最短？

(3)为使两位游客在C处相互等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？

如图，在平面直角坐标系xOy中，点A(0，3)，直线l：y＝2x－4．设圆的半径为1，圆心在l上．

(1)若圆心C也在直线y＝x－1上，过点A作圆C的切线，求切线的方程；

(2)若圆C上存在点M，使MA＝2MO，求圆心C的横坐标a的取值范围．

如图，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB．过A作AF⊥SB，垂足为F，点E，G分别是侧棱SA，SC的中点．

求证：(1)平面EFG∥平面ABC；

(2)BC⊥SA．

已知，，0＜β＜α＜π．．

(1)若，求证：；

(2)设，若，求α，β的值．

已知函数，其中a是实数．设A(x₁，f(x₁))，B(x₂，f(x₂))为该函数图象上的两点，且x₁＜x₂．

(Ⅰ)指出函数f(x)的单调区间；

(Ⅱ)若函数f(x)的图象在点A，B处的切线互相垂直，且x₂＜0，求x₂－x₁的最小值；

(Ⅲ)若函数f(x)的图象在点A，B处的切线重合，求a的取值范围．

已知椭圆C：＝1，(a＞b＞0)的两个焦点分别为F₁(－1，0)，F₂(1，0)，且椭圆C经过点．

(Ⅰ)求椭圆C的离心率；

(Ⅱ)设过点A(0，2)的直线l与椭圆C交于M、N两点，点Q是线段MN上的点，且，求点Q的轨迹方程．

如图，在三棱柱ABC－A₁B₁C中，侧棱AA₁⊥底面ABC，AB＝AC＝2AA₁，∠BAC＝120°，D，D₁分别是线段BC，B₁C₁的中点，P是线段AD的中点．

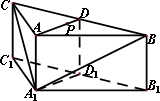
(Ⅰ)在平面ABC内，试作出过点P与平面A₁BC平行的直线l，说明理由，并证明直线l⊥平面ADD₁A₁；

(Ⅱ)设(Ⅰ)中的直线l交AB于点M，交AC于点N，求二面角A－A₁M－N的余弦值．

某算法的程序框图如图所示，其中输入的变量x在1，2，3，…，24这24个整数中等可能随机产生．

(Ⅰ)分别求出按程序框图正确编程运行时输出y的值为i的概率P_i(i＝1，2，3)；

(Ⅱ)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i(i＝1，2，3)的频数．以下是甲、乙所作频数统计表的部分数据．

当n＝2100时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i(i＝1，2，3)的频率(用分数表示)，并判断两位同学中哪一位所编写程序符合算法要求的可能性较大；

(Ⅲ)按程序框图正确编写的程序运行3次，求输出y的值为2的次数ξ的分布列及数学期望．