设函数f(x)＝alnx－bx²．

(1)若函数f(x)在x＝1处与直线y＝－相切．

①求实数a，b的值；

②求函数f(x)在[，e]上的最大值．

(2)当b＝0时，若不等式f(x)≥m＋x对所有的a∈[0，]，x∈(1，e²]都成立，求实数m的取值范围．

已知定点C(－1，0)及椭圆x²＋3y²＝5，过点C的动直线与椭圆相交于A，B两点．

(1)若线段AB中点的横坐标是，求直线AB的方程；

(2)当直线AB与x轴不垂直时，在x轴上是否存在点M，使·为常数？若存在，求出点M的坐标；若不存在，请说明理由．

已知函数，其中a是实数．设A(x₁，f(x₁))，B(x₂，f(x₂))为该函数图象上的两点，且x₁＜x₂．

(Ⅰ)指出函数f(x)的单调区间；

(Ⅱ)若函数f(x)的图象在点A，B处的切线互相垂直，且x₂＜0，证明：x₂－x₁≥1；

(Ⅲ)若函数f(x)的图象在点A，B处的切线重合，求a的取值范围．

已知圆C的方程为x²＋(y－4)²＝4，点O是坐标原点．直线l：y＝kx与圆C交于M，N两点．

(Ⅰ)求k的取值范围；

(Ⅱ)设Q(m，n)是线段MN上的点，且＝＋．请将n表示为m的函数．

如图，在三棱柱ABC－A₁B₁C中，侧棱AA₁⊥底面ABC，AB＝AC＝2AA₁＝2，∠BAC＝120°，D，D₁分别是线段BC，B₁C₁的中点，P是线段AD上异于端点的点．

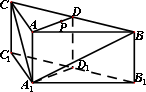
(Ⅰ)在平面ABC内，试作出过点P与平面A₁BC平行的直线l，说明理由，并证明直线l⊥平面ADD₁A₁；

(Ⅱ)设(Ⅰ)中的直线l交AC于点Q，求三棱锥A₁－QC₁D的体积．(锥体体积公式：V＝Sh，其中S为底面面积，h为高)

在△ABC中，角A，B，C的对边分别为a，b，c，且cos(A－B)cosB－sin(A－B)sin(A＋c)＝－．

(Ⅰ)求sinA的值；

(Ⅱ)若a＝4，b＝5，求向量在方向上的投影．

已知函数f(x)＝sin(ωx＋φ)(ω＞0，0＜φ＜π)的周期为π，图像的一个对称中心为，将函数f(x)图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变)，在将所得图像向右平移个单位长度后得到函数g(x)的图像．

(1)求函数f(x)与g(x)的解析式；

(2)是否存在，使得f(x₀)，g(x₀)，f(x₀)g(x₀)按照某种顺序成等差数列？若存在，请确定x₀的个数；

若不存在，说明理由．

(3)求实数a与正整数n，使得F(x)＝f(x)＋ag(x)在(0，nπ)内恰有2013个零点．

如图，在四棱柱ABCD－A₁B₁C₁D₁中，侧棱AA₁⊥底面ABCD，AB∥DC，AA₁＝1，AB＝3k，AD＝4k，BC＝5k，DC＝6k(k＞0)．

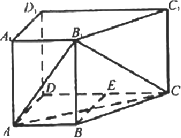
(1)求证：CD⊥平面ADD₁A₁；

(2)若直线AA₁与平面AB₁C所成角的正弦值为，求k的值；

(3)现将与四棱柱ABCD－A₁B₁C₁D₁形状和大小完全相同的两个四棱柱拼接成一个新的棱柱，规定：若拼接成的新的四棱柱形状和大小完全相同，则视为同一种拼接方案．问：共有几种不同的方案？在这些拼接成的新四棱柱中，记其中最小的表面积为f(k)，写出f(k)的表达式(直接写出答案，不必要说明理由)

如图，在正方形OABC中，O为坐标原点，点A的坐标为(10，0)，点C的坐标为(0，10)．分别将线段OA和AB十等分，分点分别记为A₁，A₂，…A₉和B₁，B₂，…B₉，连结OB_i，过A_i做x轴的垂线与OB_i交于点P_i(i∈N*，1≤i≤9)．

(1)求证：点P_i(i∈N^*，1≤i≤9)都在同一条抛物线上，并求该抛物线E的方程；

(2)过点C做直线l与抛物线E交于不同的两点M，N，若△OCM与△OCN的面积比为4∶1，求直线l的方程．

已知函数f(x)＝x－a1nx(a∈R)

(1)当a＝2时，求曲线y＝f(x)在点A(1，f(1))处的切线方程；

(2)求函数f(x)的极值．