已知函数的图象与x轴相切于点S(s，0)．

(Ⅰ)求函数f(x)的解析式；

(Ⅱ)若函数f(x)的图象与过坐标原点O的直线l相切于点T(t，f(t))，且f(t)≠0，证明：1＜t＜e；(注：e是自然对数的底)

设动点P(x，y)(x≥0)到定点的距离比到y轴的距离大．记点P的轨迹为曲线C．

(Ⅰ)求点P的轨迹方程；

(Ⅱ)设圆M过A(1，0)，且圆心M在P的轨迹上，BD是圆Ｍ在y轴的截得的弦，当M运动时弦长BD是否为定值？说明理由；

(Ⅲ)过做互相垂直的两直线交曲线C于G、H、R、S，求四边形面GRHS的最小值．

如果两个椭圆的离心率相等，那么就称这两个椭圆相似．已知椭圆C与椭圆相似，且椭圆C的一个短轴端点是抛物线的焦点．

(Ⅰ)试求椭圆C的标准方程；

(Ⅱ)设椭圆E的中心在原点，对称轴在坐标轴上，直线l∶y＝kx＋t(k≠0，t≠0)与椭圆C交于A，B两点，且与椭圆E交于H，K两点．若线段AB与线段HK的中点重合，试判断椭圆C与椭圆E是否为相似椭圆？并证明你的判断．

已知椭圆C：(a＞b＞0)的上顶点为A，两个焦点为F₁、F₂，△AF₁F₂为正三角形且周长为6．

(Ⅰ)求椭圆C的标准方程；

(Ⅱ)已知圆O：x²＋y²＝R²，若直线l与椭圆C只有一个公共点M，且直线l与圆O相切于点N；求|MN|的最大值．

将1，2，3，…，n这n个数随机排成一列，得到的一列数a₁，a₂，…，a_n称为1，2，3，…，n的一个排列．

定义为排列a₁，a₂，…，a_n的波动强度．

(Ⅰ)当n＝3时，写出排列a₁，a₂，a₃的所有可能情况及所对应的波动强度；

(Ⅱ)当n＝10时，求的最大值，给出对应的一个排列；

(Ⅲ)当n＝10时，在一个排列中交换相邻两数的位置称为一次调整，若要求每次调整时波动强度不增加，问对任意排列a₁，a₂，…，a₁₀，是否一定可以经过有限次调整使其波动强度降为9；若可以，给出调整方案，若不可以，请给出一个反例并加以说明．

已知椭圆C：(a＞b＞0)的上顶点为A，两个焦点为F₁、F₂，△AF₁F₂为正三角形且周长为6．

(Ⅰ)求椭圆C的标准方程；

(Ⅱ)已知圆O：x²＋y²＝R²，若直线l与椭圆C只有一个公共点M，且直线l与圆O相切于点N；求|MN|的最大值．

如图，在四棱锥P－ABCD中，侧面PAD是正三角形，且垂直于底面ABCD，底面ABC是边长为2的菱形，∠BAD＝60°，M为PC的中点．

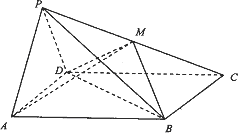
(Ⅰ)求证：PA∥平面BDM；

(Ⅱ)在AD上确定一点，使得面PB⊥面PBC，并加以证明；

(Ⅲ)求直线AC与平面ADM所成角的正弦值．

已知函数

(Ⅰ)若函数f(x)在x＝0处取到极值，求a的值．

(Ⅱ)设定义在D上的函数y＝h(x)在点P(x₀，h(x₀))处的切线方程为l：y＝g(x)，若在D内恒成立，则称P为函数的y＝h(x)的“HOLD点”．当a＝0时，试问函数y＝f(x)是否存在“HOLD点”，若存在，请至少求出一个“HOLD点”的横坐标；若不存在，请说明理由．

已知椭圆的中心在原点，焦点在x轴上，经过点，离心率．

(Ⅰ)求椭圆的方程；

(Ⅱ)椭圆的左、右顶点分别为A、B，点P为直线x＝3上任意一点(点P不在x轴上)，连结AP交椭圆于C点，连结PB并延长交椭圆于D点，试问：是否存在λ，使得S_△ACD＝λS_△BCD成立，若存在，求出λ的值；若不存在，说明理由．

已知边长为的正三角形的一个顶点位于原点，另外有两个顶点在抛物线C：x²＝2py(p＞0)上．

(1)求抛物线C的方程；

(2)已知圆过定点D(0，2)，圆心M在抛线线C上运动，且圆M与x轴交于A，B两点，设|DA|＝l，|DB|＝l₂，求的最大值．