已知函数，其中，其中ω＞0，若f(x)相邻两对称轴间的距离不小于．

(1)求ω的取值范围；

(2)在△ABC中，a、b、c分别是角A、B、C的对边，，b＋c＝3，当ω最大时，f(A)＝1，求△ABC的面积．

已知函数f(x)＝ae^x＋x²－ax，a为实常数．

(1)求证：当x＞0时，不等式f(x)＞f(－x)恒成立；

(2)求f(x)的单调区间；

(2)设斜率为k的直线与f(x)的图象交于A、B两点，其横坐标分别为x₁，x₂，若，求证：x₀＞．

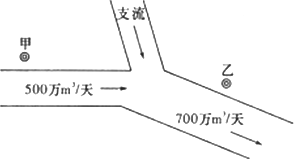
如图，在一条河流的上、下游分别有甲、乙两家化工厂，其中甲厂每天向河道内排放污水2万m³，每天流过甲厂的河水流量是500万m³(含甲厂排放的污水)；乙厂每天向河道内排放污水1.4万m³，每天流过乙厂的河水流量是700万m³(含乙厂排放的污水)．由于两厂之间有一条支流的作用，使得甲厂排放的污水在流到乙厂时；有20％可自然净化．假设工厂排放的污水能迅速与河水混合，且甲厂上游及支流均无污水排放．

(1)求河流在经过乙厂后污水含量的百分比约是多少？(精确到0.01％)

(2)根据环保要求，整个河流中污水含量不能超过0.2％，为此，甲、乙两家工厂都必须各自处理一部分污水．已知甲厂处理污水的成本是1000元/万m³，乙厂处理污水的成本是800元/万m³，

求甲、乙两厂每天应分别处理多少万m³污水，才能使两厂处理污水的总费用最小？最小总费用是多少元？

如图，ABCD是边长为2的正方形，面EAD⊥面ABCD，且EA＝ED，O是线段AD的中点，过E作直线l∥AB，F是直线l上一动点．

(1)求证：OF⊥BC；

(2)若直线l上存在唯一一点F使得直线OF与平面BCF垂直，求二面角B－OF－C的余弦值．

学校体育节拟举行一项趣味运动比赛，选手进入正赛前通过“海选”，参加海选的选手可以参加A、B、C三个测试项目，只需通过一项测试即可停止后面的测试，通过海选．甲同学通过项目A、B、C测试的概率分别为，，且通过各次测试的事件相互独立．

(1)若甲同学先测试A项目，再测试B项目，后测试C项目，求他通过海选的概率；

(2)若甲同学按某种顺序参加海选测试，第一项能通过的概率为p₁，第二项能通过的概率为p₂，第三项能通过的概率为p₃，设他通过海选时参加测试的次数为ξ，求ξ的分布列和期望(用p₁，p₂，p₃表示)．

已知向量

(1)当⊥时，求tanx的值；

(2)设函数f(x)＝(－)·，在△ABC中，角A、B、C所对的边分别为a，b，c，且f(A)＝4，a＝，求△ABC的面积S的最大值．

如图，已知半椭圆(a＞1，x≥0)的离心率为曲线C₂是以半椭圆C₁的短轴为直径的圆在y轴右侧的部分，点P(x₀，y₀)是曲线C₂上的任意一点，过点P且与曲线C₂相切的直线l与半椭圆C₁交于两个不同点A、B．

(Ⅰ)求a的值及直线l的方程(用x₀，y₀表示)；

(Ⅱ)△OAB的面积是否存在最大值？若存在，求出最大值；若不存在，说明理由．

甲、乙两名同学计划依次参加A、B、C三个公司的招聘考试，已知甲同学参加每个公司考试通过的概率为p，乙同学参加A，B，C三个公司考试通过的概率分别是，，q若甲同学至少能通过一个公司考试的概率是，甲、乙同能通过公司C考试的概率是

(Ⅰ)求p和q；

(Ⅱ)甲同学计划依次参加完三个公司的考试，乙同学计划只要能通过其中一个公司的考试就不再继续参加其它公司的考试．记甲、乙两同学按计划结束考试后能通过的考试次数分别是随机变量X和Y，求X，Y的分布列和数学期望．

如图，在六面体ABCDEFG中，平面EFG∥平面ABCD，AE⊥平面ABCD，EF⊥AE＝AB＝AD，EG＝BC，且EF＝2EG．

(Ⅰ)求证：GD∥平面BCF；

(Ⅱ)求直线AG与平面GFCD所成角的正弦值．

如图1，三棱柱中，，分别是侧棱的中点，D、E分别是、的中点．由截面DE和截面DE截去两部分后得如图2的几何体．

(1)求证：平面DE⊥平面DE；

(2)设△DE的面积为S，△DE在平面上的正投影的面积为，求；

(3)求图2中几何体的体积．