已知函数．

(1)求f(x)的最小正周期；

(2)在△ABC中，a，b，c分别是∠A、∠B、∠C的对边，若f(A)＝4，b＝1，△ABC的面积为，求a的值．

设满足以下两个条件的有穷数列a₁，a₂，…a_n为n(n＝2，3，4…)阶“期待数列”：

①a₁＋a₂＋a₃＋…＋a_n＝0；

②|a₁|＋|a₂|＋|a₃|＋…＋|a_n|＝1．

(1)若等比数列{a_n}为2k(k∈N*)阶“期待数列”，求公比q；

(2)若一个等差数列{a_n}既是2k(k∈N*)阶“期待数列”又是递增数列，求该数列的通项公式；

(3)记n阶“期待数列”{a_i}的前k项和为S_k(k＝1，2，3…，n)：

(ⅰ)求证：；

(ⅱ)若存在m∈{1，2，3…n}使，试问数列{S_i}能否为n阶“期待数列”？若能，求出所有这样的数列；若不能，请说明理由．

已知函数f(x)＝x－1nx，，(a＞0)．

(1)求函数g(x)的极值；

(2)已知x₁＞0，函数，x∈(x₁＋∞)，判断并证明h(x)的单调性；

(3)设0＜x₁＜x₂，试比较与，并加以证明．

某地区注重生态环境建设，每年用于改造生态环境总费用为x亿元，其中用于风景区改造为y亿元．该市决定建立生态环境改造投资方案，该方案要求同时具备下列三个条件：①每年用于风景区改造费用随每年改造生态环境总费用增加而增加；②每年改造生态环境总费用至少a亿元，至多b亿元；③每年用于风景区改造费用不得低于每年改造生态环境总费用的15％，但不得每年改造生态环境总费用的22％．

(1)若a＝2，b＝2.5，请你分析能否采用函数模型y＝作为生态环境改造投资方案；

(2)若a、b取正整数，并用函数模型y＝作为生态环境改造投资方案，请你求出a、b的取值．

已知函数．

(1)求f(x)的最小正周期；

(2)在△ABC中，a，b，c分别是∠A、∠B、∠C的对边，若f(A)＝4，b＝1，△ABC的面积为，求a的值．

不等式选讲选做题

已知函数f(x)＝|x＋1|||x－2|，不等式t≤f(x)在R上恒成立．

(Ⅰ)求t的取值范围；

(Ⅱ)记t的最大值为T，若正实数a，b，c满足a²＋b²＋c²＝T，求a＋2b＋c的最大值．

坐标系与参数方程选做题

在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知曲线C的参数方程为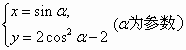，曲线D的极坐标方程为ρsin(－)＝——．

(Ⅰ)将曲线C的参数方程化为普通方程；

(Ⅱ)判断曲线C与曲线D的交点个数，并说明理由．

已知函数f(x)＝e^kx－2x(k为非零常数)．

(Ⅰ)当k＝1时，求函数f(x)的最小值；

(Ⅱ)若f(x)≥1恒成立，求k的值；

(Ⅲ)对于f(x)增区间内的三个实数x₁，x₂，x₃(其中x₁＜x₂＜x₃)，证明：．

已知四棱锥P－ABCD的三视图如下图所示，E是侧棱PC上的动点．

(1)求四棱锥P－ABCD的体积；

(2)是否不论点E在何位置，都有BD⊥AE？证明你的结论；

(3)若点E为PC的中点，求二面角D－AE－B的大小．

“肇实，正名芡实，因肇庆所产之芡实颗粒大、药力强，故名．”某科研所为进一步改良肇实，为此对肇实的两个品种(分别称为品种A和品种B)进行试验．选取两大片水塘，每大片水塘分成n小片水塘，在总共2n小片水塘中，随机选n小片水塘种植品种A，另外n小片水塘种植B．

(1)假设n＝4，在第一大片水塘中，种植品种A的小片水塘的数目记为ξ，求ξ的分布列和数学期望；

(2)试验时每大片水塘分成8小片，即n＝8，试验结束后得到品种A和品种B在每个小片水塘上的每亩产量(单位：kg/亩)如下表：

分别求品种A和品种B的每亩产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？