如图，在平面直角坐标系中，锐角α_、β的终边分别与单位圆交于A，B两点．

(Ⅰ)如果，B点的横坐标为，求cos(α＋β)的值；

(Ⅱ)若角α＋β的终边与单位圆交于C点，设角α、β、α＋β的正弦线分别为MA、NB、PC，求证：线段MA、NB、PC能构成一个三角形；

(Ⅲ)探究第(Ⅱ)小题中的三角形的外接圆面积是否为定值？若是，求出该定值；若不是，请说明理由．

如图，三棱柱ABC－A₁B₁C₁中，AA₁⊥平面ABC，∠BAC＝90°，AB＝2，AC＝6，点D在线段BB₁上，且BD＝BB₁，A₁C∩AC₁＝E．

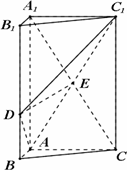
(Ⅰ)求证：直线DE与平面ABC不平行；

(Ⅱ)设平面ADC₁与平面ABC所成的锐二面角为，若cos＝，求AA₁的长；

(Ⅲ)在(Ⅱ)的条件下，设平面ADC₁∩平面ABC＝l，求直线l与DE所成的角的余弦值．

已知函数f(x)＝ln(x＋1)＋(a∈R)．

(Ⅰ)当a＝2时，求函数y＝f(x)的图象在x＝0处的切线方程；

(Ⅱ)判断函数f(x)的单调性；

(Ⅲ)若函数f(x)在(a，a＋1)上为增函数，求a的取值范围．

如图，圆C与y轴相切于点T(0，2)，与x轴正半轴相交于两点M，N(点M在点N的左侧)，且|MN|＝3．

(Ⅰ)求圆C的方程；

(Ⅱ)过点M任作一条直线与椭圆г：＋＝1相交于A、B两点，连接AN、BN，求证：∠ANM＝∠BNM．

已知四棱锥P－ABCD的三视图如图所示，△PBC为正三角形．

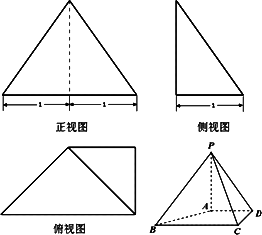
(Ⅰ)在平面PCD中作一条与底面ABCD平行的直线，并说明理由；

(Ⅱ)求证：AC⊥平面PAB；

(Ⅲ)求三棱锥A－PBC的高．

已知F(1，0)，P是平面上一动点，P到直线l：x＝－1上的射影为点N，且满足(＋)·＝0

(1)求点P的轨迹C的方程；

(2)过点M(1，2)作曲线C的两条弦MA，MB，设MA，MB所在直线的斜率分别为k₁，k₂，当k₁，k₂变化且满足k₁＋k₂＝－1时，证明直线AB恒过定点，并求出该定点坐标．

已知函数f(x)＝x³－x²＋ax＋b(a，b∈R)的一个极值点为x＝1．

(1)求a的值和f(x)的单调区间；

(2)若方程x²＝bx－ab＝0的两个实根为α，β(α＜β)，函数f(x)在区间[α，β]上单调，求b的取值范围．

在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE∶EB＝CF∶FA＝CP∶PB＝1∶2(如图1)．将△AEF沿EF折起到△A₁EF的位置，使二面角A₁－EF－B成直二面角，连结A₁B、A₁P(如图2)

(Ⅰ)求证：A₁E⊥平面BEP；

(Ⅱ)求直线A₁E与平面A₁BP所成角的大小．

函数(a∈R)

(Ⅰ)当时，求f(x)的单调区间；

(Ⅱ)若，若m，n分别为f(x)的极大值和极小值，若S＝m－n，求S取值范围．

如图，AC是圆O的直径，点B在圆O上，∠BAC＝30°，BM⊥AC交AC于点M，EA⊥平面ABC，FC∥EA，AC＝4，EA＝3，FC＝1．

(I)证明：EM⊥BF；

(II)求平面BEF与平面ABC所成锐二面角的余弦值．