如图，某地质队自水平地面A，B，C三处垂直向地下钻探，自A点向下钻到A₁处发现矿藏，再继续下钻到A₂处后下面已无矿，从而得到在A处正下方的矿层厚度为A₁A₂＝d₁．同样可得在B，C处正下方的矿层厚度分别为B₁B₂＝d₂，C₁C₂＝d₃，且d₁＜d₂＜d₃．过AB，AC的中点M，N且与直线AA₂平行的平面截多面体A₁B₁C₁－A₂B₂C₂所得的截面DEFG为该多面体的一个中截面，其面积记为S_中．

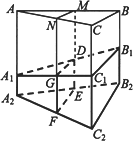
(Ⅰ)证明：中截面DEFG是梯形；

(Ⅱ)在△ABC中，记BC＝a，BC边上的高为h，面积为S．在估测三角形ABC区域内正下方的矿藏储量(即多面体A₁B₁C₁－A₂B₂C₂的体积V)时，可用近似公式V_估＝S_中·h来估算．已知V＝(d₁＋d₂＋d₃)S，试判断V_估与V的大小关系，并加以证明．

过抛物线E：x²＝2py(p＞0)的焦点F作斜率分别为k₁，k₂的两条不同的直线l₁，l₂，且k₁＋k₂＝2，l₁与E相交于点A，B，l₂与E相交于点C，D．以AB，CD为直径的圆M，圆N(M，N为圆心)的公共弦所在的直线记为l．

(Ⅰ)若k₁＞0，k₂＞0，证明；；

(Ⅱ)若点M到直线l的距离的最小值为，求抛物线E的方程．

在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”．如图所示的路径MM₁M₂M₃N与路径MN₁N都是M到N的“L路径”．某地有三个新建的居民区，分别位于平面xOy内三点A(3，20)，B(－10，0)，C(14，0)处．现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心．

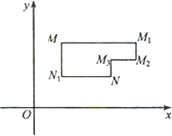
(Ⅰ)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明)；

(Ⅱ)若以原点O为圆心，半径为1的圆的内部是保护区，“L路径”不能进入保护区，请确定点P的位置，使其到三个居民区的“L路径”长度值和最小．

已知函数f(x)＝|e^x－bx|，其中e为自然对数的底．

(1)当b＝1时，求曲线y＝f(x)在x＝1处的切线方程；

(2)若函数y＝f(x)有且只有一个零点，求实数b的取值范围；

(3)当b＞0时，判断函数y＝f(x)在区间(0，2)上是否存在极大值，若存在，求出极大值及相应实数b的取值范围．

已知函数f(x)＝e^x－x(e为自然对数的底数)．

(1)求f(x)的最小值；

(2)不等式f(x)＞ax的解集为P，若M＝{x|≤x≤2}且M∩P≠求实数a的取值范围；

(3)已知n∈N^*，且S_n＝，是否存在等差数列{a_n}和首项为f(1)公比大于0的等比数列{b_n}，使得a₁＋a₂＋…＋a_n＋b₁＋b₂＋…b_n＝S_n？若存在，请求出数列{a_n}、(b_n)的通项公式．若不存在，请说明理由．

已知函数f(x)＝lnx＋(a∈R)．

(1)当时，如果函数g(x)＝f(x)－k仅有一个零点，求实数k的取值范围；

(2)当a＝2时，试比较f(x)与1的大小；

(3)求证：(n∈N^*)．

已知f(x)＝ax－lnx，a∈R．

(Ⅰ)当a＝2时，求曲线f(x)在点(1，f(1))处的切线方程；

(Ⅱ)若f(x)在x＝1处有极值，求f(x)的单调递增区间；

(Ⅲ)是否存在实数a，使f(x)在区间(0，e]的最小值是3，若存在，求出a的值；若不存在，说明理由．

已知f(x)＝ax＋＋2－2a(a＞0)的图像在点(1，f(1))处的切线与直线y＝2x＋1平行．

(1)求a，b满足的关系式；

(2)若f(x)≥2lnx在[1，＋∞)上恒成立，求a的取值范围；

(3)证明：1＋＋＋…＋＞(2n＋1)＋(n∈₊)

已知函数f(x)＝(－1)²＋(－1)²的定义域为[m，n)且1≤m＜n≤2．

(1)讨论函数f(x)的单调性；

(2)证明：对任意x₁、x₂∈[m，n]，不等式?|f(x₁)－f(x₂)|＜1恒成立．

已知二次函数y＝g(x)的图象经过点O(0，0)、A(m，0)与点P(m＋1，m＋1)，设函数f(x)＝(x－n)g(x)在x＝a和x＝b处取到极值，其中m＞n＞0，b＜a．

(1)求g(x)的二次项系数k的值；

(2)比较a，b，m，n的大小(要求按从小到大排列)；

(3)若m＋n≤2，且过原点存在两条互相垂直的直线与曲线y＝f(x)均相切，求y＝f(x)．