选修4－1：平面几何选讲

如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC＝ED．

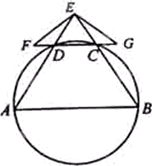
(Ⅰ)证明：CD∥AB；

(Ⅱ)延长CD到F，延长DC到G，使得EF＝EG，证明：A，B，G，F四点共圆．

图1，平面四边形ABCD关于直线AC对称，∠A＝60°，∠C＝90°，CD＝2，把△ABD沿BD折起(图2)，使二面角A―BD―C的余弦值等于．对于图2，完成以下各小题：

(1)求A，C两点间的距离；

(2)证明：AC⊥平面BCD；

(3)求直线AC与平面ABD所成角的正弦值．

如图，直线AB过圆心O，交圆O于A、B，直线AF交圆O于F(不与B重合)，直线l与圆O相切于C，交AB于E，且与AF垂直，垂足为G，连接AC．

求证：(Ⅰ)∠BAC＝∠CAG；

(Ⅱ)AC²＝AE·AF．

如图：PA⊥平面ABCD，ABCD是矩形，PA＝AB＝1，点E、F分别是BC、PB的中点．

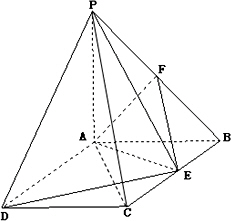
(Ⅰ)证明：EF∥平面PAC；

(Ⅱ)当AD等于何值时，二面角P－DE－A的大小为30°；

(Ⅲ)求二面角P－DE－A余弦值的取值范围．

几何证明选讲：

如图，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F．

求证：(1)BE·DE＋AC·CE＝CE²；

(2)∠EDF＝∠CDB：

(3)E．F，C，B四点共圆求圆是参数)截得的弦长．

如图，四棱锥S－ABCD的底面ABCD是正方形，侧面SAB是等腰三角形且垂直于底面，SA＝SB＝，AB＝2，E、F分别是AB、SD的中点．

(Ⅰ)求证：EF∥平面SBC：

(Ⅱ)求二面角F－CE－A的大小．

如图，在矩形ABCD中，AB＝2BC＝4，点M在边DC上，点F在边AB上，且DE⊥AM，垂足为E，若将△ADM沿AM折起，使点D位于位置，连接得四棱锥．

(1)求证：；

(2)若是正三角形，求四棱锥的体积．

如图，三棱柱ABC－A₁B₁C₁中，CA＝CB，AB＝AA₁，∠BAA₁＝60°．

(Ⅰ)证明AB⊥A₁C；

(Ⅱ)若平面ABC⊥平面AA₁B₁B，AB＝CB＝2，求直线A₁C与平面BB₁C₁C所成角的正弦值．

如图，在△ABC中，∠ABC＝90°，AB＝，BC＝1，P为△ABC内一点，∠BPC＝90°

(1)若PB＝，求PA；

(2)若∠APB＝150°，求tan∠PBA

如图，已知AB⊥平面ACD，DE∥AB，△ACD是正三角形，AD＝DE＝2AB，且F是CD的中点．

(1)求证：AF∥平面BCE；

(2)求证：平面BCE⊥平面CDE；

(3)求平面BCE与平面ACD所成锐二面角的大小．