
科目: 来源: 题型:单选题
设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在 上的零点个数为( )
上的零点个数为( )
| A.5 | B.6 | C.7 | D.8 |
查看答案和解析>>
科目: 来源: 题型:单选题
如图,设点A是单位圆上的一定点,动点P从A出发在圆上按逆时针方向旋转一周,点P所转过的弧AP的长为l,弦AP的长度为d,则函数d=f(l)的图象大致是( )

查看答案和解析>>
科目: 来源: 题型:单选题
若对于定义在R上的函数f(x),其图象是连续不断的,且存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数都成立,则称f(x)是一个“λ伴随函数”.下列关于“λ伴随函数”的结论:①f(x)=0不是常数函数中唯一一个“λ伴随函数”;②f(x)=x不是“λ伴随函数”;③f(x)=x2是“λ伴随函数”;④“ 伴随函数”至少有一个零点.其中正确的结论个数是( )
伴随函数”至少有一个零点.其中正确的结论个数是( )
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目: 来源: 题型:单选题
如图甲是某条公共汽车线路收支差额 与乘客量
与乘客量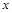 的图象(收支差额=车票收入—支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)是不改变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,提高车票价格.下面给出四个图象:在这些图象中( )
的图象(收支差额=车票收入—支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)是不改变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,提高车票价格.下面给出四个图象:在这些图象中( )
| A.①反映了建议(Ⅱ),③反映了建议(Ⅰ) |
| B.①反映了建议(Ⅰ),③反映了建议(Ⅱ) |
| C.②反映了建议(Ⅰ),④反映了建议(Ⅱ) |
| D.④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
查看答案和解析>>
科目: 来源: 题型:单选题
已知函数f(x)是定义在R上的奇函数,且当x∈(-∞,0]时,f(x)=e-x-ex2+a,则函数f(x)在x=1处的切线方程为( )
| A.x+y=0 | B.ex-y+1-e=0 |
| C.ex+y-1-e=0 | D.x-y=0 |
查看答案和解析>>
科目: 来源: 题型:单选题
定义在R上的函数的图象关于点 成中心对称,且对任意的实数x都有f(x)=-f
成中心对称,且对任意的实数x都有f(x)=-f ,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2013)=( )
,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2013)=( )
| A.0 | B.-2 |
| C.1 | D.-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com