
科目: 来源: 题型:解答题
(2013•湖北)设a>0,b>0,已知函数f(x)= .
.
(1)当a≠b时,讨论函数f(x)的单调性;
(2)当x>0时,称f(x)为a、b关于x的加权平均数.
(1)判断f(1),f( ),f(
),f( )是否成等比数列,并证明f(
)是否成等比数列,并证明f( )≤f(
)≤f( );
);
(2)a、b的几何平均数记为G.称 为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
查看答案和解析>>
科目: 来源: 题型:解答题
(2013•浙江)已知a∈R,函数f(x)=x3﹣3x2+3ax﹣3a+3.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈[0,2]时,求|f(x)|的最大值.
查看答案和解析>>
科目: 来源: 题型:解答题
已知函数 a为常数且a>0.
a为常数且a>0.
(1)证明:函数f(x)的图像关于直线x= 对称;
对称;
(2)若x0满足f(f(x0))= x0,但f(x0)≠x0,则x0称为函数f(x)的二阶周期点,如果f(x)有两个二阶周期点x1,x2,试确定a的取值范围;
(3)对于(2)中的x1,x2,和a,设x3为函数f(f(x))的最大值点,A(x1,f(f(x1))),B(x2,f(f(x2))),C(x3,0),记△ABC的面积为S(a),讨论S(a)的单调性.
查看答案和解析>>
科目: 来源: 题型:解答题
(2013•湖北)设n是正整数,r为正有理数.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(2)证明: ;
;
(3)设x∈R,记[x]为不小于x的最小整数,例如 .令
.令 的值.
的值.
(参考数据: .
.
查看答案和解析>>
科目: 来源: 题型:解答题
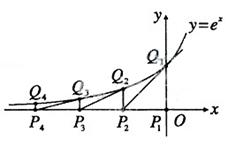
如图,从点P1(0,0)作 轴的垂线交曲线
轴的垂线交曲线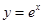 于点
于点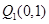 ,曲线在
,曲线在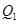 点处的切线与
点处的切线与 轴交于点
轴交于点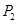 .再从
.再从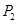 做
做 轴的垂线交曲线于点
轴的垂线交曲线于点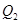 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: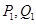 ;
;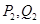 ;…;
;…; ,记
,记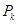 点的坐标为
点的坐标为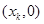 (
(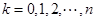 ).
).
(1)试求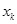 与
与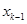 的关系(
的关系(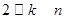 );
);
(2)求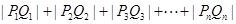 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
已知 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间[-1,4]上的最大值是12.
在区间[-1,4]上的最大值是12.
(1)求f(x)的解析式;
(2)是否存在正整数m,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
(2013•重庆)某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目: 来源: 题型:解答题
(2011•山东)某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为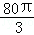 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
(1)写出y关于r的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com