设是实数，
（1）试确定的值，使成立；
（2）求证：不论为何实数，均为增函数

函数（为常数）的图象过原点，且对任意总有成立；
（1）若的最大值等于1，求的解析式；
（2）试比较与的大小关系.

已知函数的定义域为，
（1）求；
（2）若，且，求实数的取值范围.

若函数为定义域上的单调函数,且存在区间(其中,使得当时, 的取值范围恰为,则称函数是上的正函数,区间叫做函数的等域区间.
（1）已知是上的正函数，求的等域区间；
（2）试探求是否存在，使得函数是上的正函数？若存在，请求出实数的取值范围；若不存在，请说明理由.

已知函数，恒过定点．
（1）求实数；
（2）在（1）的条件下，将函数的图象向下平移1个单位，再向左平移个单位后得到函数，设函数的反函数为，直接写出的解析式；
（3）对于定义在上的函数，若在其定义域内，不等式恒成立，求实数的取值范围．

湖南省环保研究所对长沙市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数与时刻x的关系为，其中a是与气象有关的参数，且，若用每天的最大值作为当天的综合放射性污染指数，并记作.
(Ⅰ)令，求t的取值范围；
(Ⅱ)省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？

设，是上的奇函数．
（Ⅰ）求的值；
（Ⅱ）证明：在上为增函数；
（Ⅲ）解不等式：．

已知函数，.
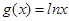（1）如果函数在上是单调减函数，求的取值范围；
（2）是否存在实数，使得方程在区间内有且只有两个不相等的实数根？若存在，请求出的取值范围；若不存在，请说明理由．

已知函数，.
（1）若，是否存在、，使为偶函数，如果存在，请举例并证明你的结论，如果不存在，请说明理由；
（2）若，，求在上的单调区间；
（3）已知，对，，有成立，求的取值范围.

已知函数.
（1）当时，判断的奇偶性，并说明理由；
（2）当时，若，求的值；
（3）若，且对任何不等式恒成立，求实数的取值范围．