
科目: 来源: 题型:解答题
已知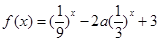
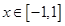
(1)若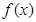 的最小值记为
的最小值记为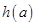 ,求
,求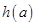 的解析式.
的解析式.
(2)是否存在实数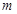 ,
,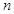 同时满足以下条件:①
同时满足以下条件:① ;②当
;②当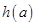 的定义域为[
的定义域为[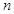 ,
,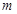 ]时,值域为[
]时,值域为[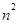 ,
,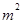 ];若存在,求出
];若存在,求出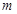 ,
,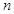 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
已知函数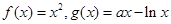 ,
,
(1)若函数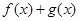 在
在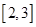 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(2)是否存在实数 ,当
,当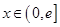 (
(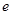 是自然常数)时,函数
是自然常数)时,函数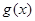 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当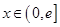 时,证明:
时,证明: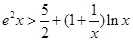 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度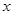 (单位:cm)满足关系:
(单位:cm)满足关系: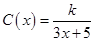 (
(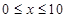 ,
,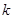 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设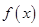 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求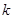 的值及
的值及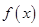 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用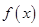 达到最小?并求出最小值.
达到最小?并求出最小值.
查看答案和解析>>
科目: 来源: 题型:解答题
已知函数f(x)=lnx+a ,其中a为大于零的常数.
,其中a为大于零的常数.
(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证:对于任意的n∈N*,且n>1时,都有lnn> +
+ +…+
+…+ 恒成立.
恒成立.
查看答案和解析>>
科目: 来源: 题型:解答题
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如表:
| 时间(将第x天记为x)x | 1 | 10 | 11 | 18 |
| 单价(元/件)P | 9 | 0 | 1 | 8 |
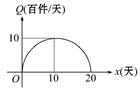
查看答案和解析>>
科目: 来源: 题型:解答题
(2014·孝感模拟)已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x- +
+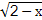 .
.
(1)求函数f(x)的最小值.
(2)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com