某创业投资公司拟投资开发某种新能源产品，估计能获得10万元到1 000万元的投资收益．现准备制定一个对科研课题组的奖励方案：资金y(单位：万元)随投资收益x(单位：万元)的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%.
(1)若建立函数y＝f(x)模型制定奖励方案，试用数学语言表述该公司对奖励函数f(x)模型的基本要求，并分析函数y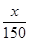＝＋2是否符合公司要求的奖励函数模型，并说明原因；
(2)若该公司采用模型函数y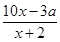＝作为奖励函数模型，试确定最小的正整数a的值．

某商场对A品牌的商品进行了市场调查，预计2012年从1月起前x个月顾客对A品牌的商品的需求总量P(x)件与月份x的近似关系是：
P(x)＝x(x＋1)(41－2x)(x≤12且x∈N^*)
(1)写出第x月的需求量f(x)的表达式；
(2)若第x月的销售量g(x)＝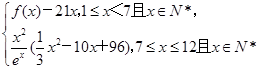
(单位：件)，每件利润q(x)元与月份x的近似关系为：q(x)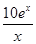＝，问：该商场销售A品牌商品，预计第几月的月利润达到最大值？月利润最大值是多少？(e⁶≈403)

经市场调查，某旅游城市在过去的一个月内(以30天计)，旅游人数f(t)(万人)与时间t(天)的函数关系近似满足f(t)＝4＋，人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)＝115－|t－15|.
(1)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30，t∈N^*)的函数关系式；
(2)求该城市旅游日收益的最小值(万元)．

设函数f(x)＝ax²＋bx＋b－1(a≠0)．
(1)当a＝1，b＝－2时，求函数f(x)的零点；
(2)若对任意b∈R，函数f(x)恒有两个不同零点，求实数a的取值范围．

已知二次函数f(x)＝ax²＋bx＋1(a>0)，F(x)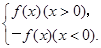＝若f(－1)＝0，且对任意实数x均有f(x)≥0成立．
(1)求F(x)的表达式；
(2)当x∈[－2,2]时，g(x)＝f(x)－kx是单调函数，求k的取值范围．

已知函数f(x)＝x²＋bx＋c(b，c∈R)，对任意的x∈R，恒有f′(x)≤f(x)．
(1)证明：当x≥0时，f(x)≤(x＋c)²；
(2)若对满足题设条件的任意b，c，不等式f(c)－f(b)≤M(c²－b²)恒成立，求M的最小值．

为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层，某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元，该建筑物每年的能源消耗费用C(单位：万元)与隔热层厚度x(单位：cm)满足关系：C(x)＝ (0≤x≤10)，若不建隔热层，每年能源消耗费用为8万元．设f(x)为隔热层建造费用与20年的能源消耗费用之和．
(1)求k的值及f(x)的表达式；
(2)隔热层修建多厚时，总费用f(x)达到最小，并求最小值．

已知函数f(x)＝的图象过原点，且关于点(－1,2)成中心对称．
(1)求函数f(x)的解析式；
(2)若数列{a_n}满足a₁＝2，a_n＋1＝f(a_n)，试证明数列为等比数列，并求出数列{a_n}的通项公式．

已知二次函数f(x)的二次项系数为a，且不等式f(x)＞2x的解集为(－1,3)．
(1)若函数g(x)＝xf(x)在区间内单调递减，求a的取值范围；
(2)当a＝－1时，证明方程f(x)＝2x³－1仅有一个实数根；
(3)当x∈[0,1]时，试讨论|f(x)＋(2a－1)x＋3a＋1|≤3成立的充要条件．

某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本为C(x)．当年产量不足80千件时，C(x)＝x²＋10x(万元)；当年产量不小于80千件时，C(x)＝51x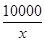＋－1 450(万元)，每件商品售价为0.05万元，通过市场分析，该厂生产的商品能全部售完．
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式；
(2)当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？