
科目: 来源: 题型:解答题
已知幂函数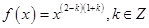 ,且
,且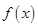 在
在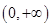 上单调递增.
上单调递增.
(1)求实数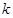 的值,并写出相应的函数
的值,并写出相应的函数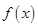 的解析式;
的解析式;
(2)若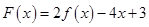 在区间
在区间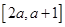 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)试判断是否存在正数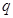 ,使函数
,使函数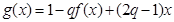 在区间
在区间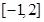 上的值域为
上的值域为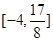 若存在,求出
若存在,求出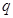 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙,地面利用原地面均不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,屋顶每平方米造价20元.
(1)仓库面积 的最大允许值是多少?
的最大允许值是多少?
(2)为使面积 达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
达到最大而实际投入又不超过预算,正面铁栅应设计为多长?
查看答案和解析>>
科目: 来源: 题型:解答题
如果函数f(x)的定义域为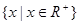 ,且f(x)为增函数,f(xy)=f(x)+f(y)。
,且f(x)为增函数,f(xy)=f(x)+f(y)。
(1)证明: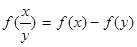 ;
;
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围。
查看答案和解析>>
科目: 来源: 题型:解答题
已知函数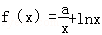 ,g(x)=
,g(x)=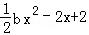 ,a,b∈R.
,a,b∈R.
(1)求函数f(x)的单调区间;
(2)记函数h(x)=f(x)+g(x),当a=0时,h(x)在(0,1)上有且只有一个极值点,求实数b的取值范围;
(3)记函数F(x)=|f(x)|,证明:存在一条过原点的直线l与y=F(x)的图象有两个切点.
查看答案和解析>>
科目: 来源: 题型:解答题
某人2002年底花100万元买了一套住房,其中首付30万元,70万元采用商业贷款.贷款的月利率为5‰,按复利计算,每月等额还贷一次,10年还清,并从贷款后的次月开始还贷.
(1)这个人每月应还贷多少元?
(2)为了抑制高房价,国家出台“国五条”,要求卖房时按照差额的20%缴税.如果这个人现在将住房150万元卖出,并且差额税由卖房人承担,问:卖房人将获利约多少元?(参考数据:(1+0.005)120≈1.8)
查看答案和解析>>
科目: 来源: 题型:解答题
某水域一艘装载浓硫酸的货船发生侧翻,导致浓硫酸泄漏,对河水造成了污染.为减少对环境的影响,环保部门迅速反应,及时向污染河道投入固体碱, 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度 与时间
与时间 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用.
(Ⅰ) 如果只投放1个单位的固体碱,则能够维持有效的抑制作用的时间有多长?
(Ⅱ) 第一次投放1单位固体碱后,当污染河道水中的碱浓度减少到 时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为
时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为 ,求
,求 的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com