
科目: 来源: 题型:解答题
已知函数f(x)=|x-a|.
(Ⅰ)若不等式f(x)≥3的解集为{x|x≤1或x≥5},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+4)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:解答题
某品牌电视生产厂家有A、B两种型号的电视机参加了家电下乡活动,若厂家A、B对两种型号的电视机的投放金额分别为p、q万元,农民购买电视机获得的补贴分别为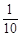 p、
p、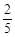 lnq万元,已知A、B两种型号的电视机的投放总额为10万元,且A、B两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据:
lnq万元,已知A、B两种型号的电视机的投放总额为10万元,且A、B两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据: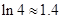 ).
).
查看答案和解析>>
科目: 来源: 题型:解答题
已知奇函数f(x)=
(1)求实数m的值,并在给出的直角坐标系中画出y=f(x)的图象;
(2)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围.
查看答案和解析>>
科目: 来源: 题型:解答题
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x( ≥10)层,则每平方米的平均建筑费用为560+48
≥10)层,则每平方米的平均建筑费用为560+48 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
查看答案和解析>>
科目: 来源: 题型:解答题
已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
(I)求f(x)的解析式;
(II)已知k的取值范围为[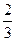 ,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
为了保护水资源,提倡节约用水,某市对居民生活用水收费标准如下:每户每月用水不超过6吨时每吨3元,当用水超过6吨但不超过15吨时,超过部分每吨5元,当用水超过15吨时,超过部分每吨10元。
(1)求水费y(元)关于用水量x(吨)之间的函数关系式;
(2)若某户居民某月所交水费为93元,试求此用户该月的用水量。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com