
科目: 来源:专项题 题型:解答题
查看答案和解析>>
科目: 来源:专项题 题型:解答题
查看答案和解析>>
科目: 来源:专项题 题型:解答题
查看答案和解析>>
科目: 来源:江西省高考真题 题型:单选题


查看答案和解析>>
科目: 来源:湖南省高考真题 题型:解答题
查看答案和解析>>
科目: 来源:福建省高考真题 题型:单选题
 对称,据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程m[f(x)]2+nf(x)+p=0的解集都不可能是
对称,据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程m[f(x)]2+nf(x)+p=0的解集都不可能是[ ]
查看答案和解析>>
科目: 来源:专项题 题型:解答题
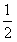 x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元,
x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元, 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com