
科目: 来源:江苏高考真题 题型:解答题
 的最大值为g(a)。
的最大值为g(a)。 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t); 的所有实数a。
的所有实数a。查看答案和解析>>
科目: 来源:陕西省高考真题 题型:单选题
[ ]
查看答案和解析>>
科目: 来源:江苏高考真题 题型:解答题
查看答案和解析>>
科目: 来源:高考真题 题型:单选题
 的一个单调增区间是
的一个单调增区间是 A.
B.
C.
D.
查看答案和解析>>
科目: 来源:四川省高考真题 题型:解答题
查看答案和解析>>
科目: 来源:专项题 题型:解答题
查看答案和解析>>
科目: 来源:专项题 题型:解答题
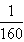 (x-40)2+100万元(已扣除投资,下同)。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在未来10年内对该项目每年都投入60万元的销售资金,其中在前5年中,每年都从60万元中拨出30万元用于修建一条公路。公路5年建成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获纯利润Q=
(x-40)2+100万元(已扣除投资,下同)。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在未来10年内对该项目每年都投入60万元的销售资金,其中在前5年中,每年都从60万元中拨出30万元用于修建一条公路。公路5年建成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获纯利润Q=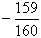 (60-x)2+
(60-x)2+ (60-x)万元,问仅从这10年的累积利润看,该规划方案是否可行?
(60-x)万元,问仅从这10年的累积利润看,该规划方案是否可行?查看答案和解析>>
科目: 来源:湖北省高考真题 题型:解答题
 的大小,并说明理由。
的大小,并说明理由。查看答案和解析>>
科目: 来源:福建省高考真题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com