（14分）（2011•陕西）设f（x）=lnx，g（x）=f（x）+f′（x）．
（Ⅰ）求g（x）的单调区间和最小值；
（Ⅱ）讨论g（x）与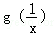的大小关系；
（Ⅲ）求a的取值范围，使得g（a）﹣g（x）＜对任意x＞0成立．

（12分）（2011•陕西）如图，从点P₁（0，0）做x轴的垂线交曲线y=e^x于点Q₁（0，1），曲线在Q₁点处的切线与x轴交于点P₂，再从P₂做x轴的垂线交曲线于点Q₂，依次重复上述过程得到一系列点：P₁，Q₁；P₂，Q₂…；P_n，Q_n，记P_k点的坐标为（x_k，0）（k=1，2，…，n）．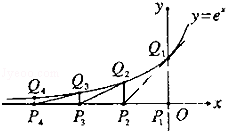

（Ⅰ）试求x_k与x_k﹣1的关系（2≤k≤n）；
（Ⅱ）求|P₁Q₁|+|P₂Q₂|+|P₃Q₃|+…+|P_nQ_n|．

（14分）（2011•广东）设a＞0，讨论函数f（x）=lnx+a（1﹣a）x²﹣2（1﹣a）x的单调性．

（14分）（2011•福建）已知a，b为常数，且a≠0，函数f（x）=﹣ax+b+axlnx，f（e）=2（e=2.71828…是自然对数的底数）．
（I）求实数b的值；
（II）求函数f（x）的单调区间；
（III）当a=1时，是否同时存在实数m和M（m＜M），使得对每一个t∈[m，M]，直线y=t与曲线y=f（x）（x∈[，e]）都有公共点？若存在，求出最小的实数m和最大的实数M；若不存在，说明理由．

（13分）（2011•重庆）设f（x）=x³+ax²+bx+1的导数f′（x）满足f′（1）=2a，f′（2）=﹣b，其中常数a，b∈R．
（Ⅰ）求曲线y=f（x）在点（1，f（1））处的切线方程．
（Ⅱ）设g（x）=f′（x）e^﹣x．求函数g（x）的极值．

已知函数,.
(1)讨论在内和在内的零点情况.
(2)设是在内的一个零点,求在上的最值.
(3)证明对恒有.[来

设函数.
（1）若在时有极值，求实数的值和的极大值；
（2）若在定义域上是增函数,求实数的取值范围．

已知．
若曲线在处的切线与直线平行，求a的值；
当时，求的单调区间．

已知函数．
（1）若函数在时取得极值，求实数的值；
（2）若对任意恒成立，求实数的取值范围．

某分公司经销某种品牌产品，每件产品的成本为元，并且每件产品需向总公司交元的管理费，预计当每件产品的售价为元()时，一年的销售量为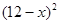万件．
（1）求该分公司一年的利润(万元)与每件产品的售价的函数关系式；
（2）当每件产品的售价为多少元时，该分公司一年的利润最大？并求出的最大值．