已知函数.
（Ⅰ）若,求在点处的切线方程；
（Ⅱ）求函数的极值点；
（Ⅲ）若恒成立，求的取值范围.

已知函数.
（Ⅰ）若，求在点处的切线方程；
（Ⅱ）求函数的极值点.

已知函数，其中是自然对数的底数，.
（Ⅰ）求函数的单调区间；
（Ⅱ）当时，求函数的最小值.

已知函数，其中是自然对数的底数，.
（Ⅰ）求函数的单调区间；
（Ⅱ）当时，试确定函数的零点个数，并说明理由.

已知函数f（x）=lnx－ax（a>0）．
（I）当a=2时，求f（x）的单调区间与极值；
（Ⅱ）若对于任意的x∈（0，+），都有f（x）<0，求a的取值范围．

已知，函数．
（Ⅰ）当时，求的最小值；
（Ⅱ）若在区间上是单调函数，求的取值范围．

已知函数．
（1）证明函数在区间上单调递减；
（2）若不等式对任意的都成立，（其中是自然对数的底数），求实数的最大值．

已知a，b为常数，a¹0，函数．
（1）若a=2，b=1，求在（0，+∞）内的极值；
（2）①若a>0，b>0，求证：在区间[1，2]上是增函数；
②若，，且在区间[1，2]上是增函数，求由所有点形成的平面区域的面积．

甲、乙两地相距1000，货车从甲地匀速行驶到乙地，速度不得超过80，已知货车每小时的运输成本（单位：元）由可变成本和固定成本组成，可变成本是速度平方的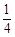倍，固定成本为a元．
（1）将全程运输成本y（元）表示为速度v（）的函数，并指出这个函数的定义域；
（2）为了使全程运输成本最小，货车应以多大的速度行驶？

已知a，b为常数，a¹0，函数．
（1）若a=2，b=1，求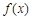在（0，+∞）内的极值；
（2）①若a>0，b>0，求证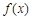：在区间[1，2]上是增函数；
②若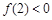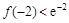，，且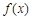在区间[1，2]上是增函数，求由所有点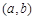形成的平面区域的面积．