
科目: 来源: 题型:填空题
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图4中的实心点个数1,5,12,22,…, 被称为五角形数,其中第1个五角形数记作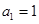 ,第2个五角形数记作
,第2个五角形数记作 ,第3个五角形数记作
,第3个五角形数记作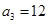 ,第4个五角形数记作
,第4个五角形数记作 ,……,若按此规律继续下去,若
,……,若按此规律继续下去,若 ,则
,则 .
.
1 5 12 22
查看答案和解析>>
科目: 来源: 题型:填空题
挪威数学家阿贝尔,曾经根据阶梯形图形的两种不同分割(如下图),利用它们的面积关系发现了一个重要的恒等式——阿贝尔公式: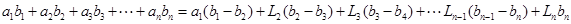
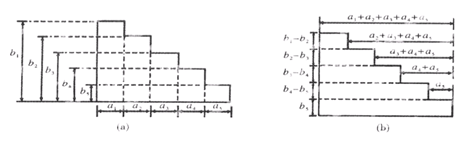
则其中:(I)L3= ;(Ⅱ)Ln= .
查看答案和解析>>
科目: 来源: 题型:填空题
.根据下面一组等式
S1=1
S2=2+3=5
S3=4+5+6=15
S4=7+8+9+10=34
S5=11+12+13+14+15=65
S6=16+17+18+19+20+21=111
S7=22+23+24+25+26+27+28=175
… … … … … … … …
可得 .
.
查看答案和解析>>
科目: 来源: 题型:填空题
对于数列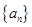
 ,若
,若 中最大值
中最大值 ,则称数列
,则称数列 为数列
为数列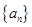 的“凸值数列”.如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有___________________.
的“凸值数列”.如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有___________________.
①递减数列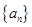 的“凸值数列”是常数列;②不存在数列
的“凸值数列”是常数列;②不存在数列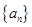 ,它的“凸值数列”还是
,它的“凸值数列”还是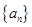 本身;③任意数列
本身;③任意数列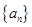 的“凸值数列”是递增数列;④“凸值数列”为1,3,3,9的所有数列
的“凸值数列”是递增数列;④“凸值数列”为1,3,3,9的所有数列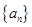 的个数为3.
的个数为3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com