
科目: 来源: 题型:解答题
如图,已知正方形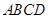 的边长为
的边长为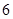 ,点
,点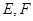 分别在边
分别在边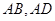 上,
上,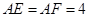 ,现将△
,现将△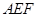 沿线段
沿线段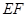 折起到△
折起到△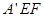 位置,使得
位置,使得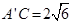 .
.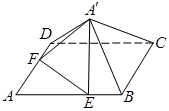
(1)求五棱锥 的体积;
的体积;
(2)在线段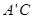 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面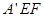 ?若存在,求
?若存在,求 ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1﹣A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(1)证明:中截面DEFG是梯形;
(2)在△ABC中,记BC=a,BC边上的高为h,面积为S.在估测三角形ABC区域内正下方的矿藏储量(即多面体A1B1C1﹣A2B2C2的体积V)时,可用近似公式V估=S中﹣h来估算.已知V= (d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.
(d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.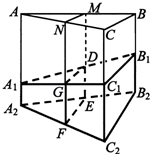
查看答案和解析>>
科目: 来源: 题型:解答题
(2013•浙江)如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2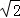 .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(1)证明:PQ∥平面BCD;
(2)若二面角C﹣BM﹣D的大小为60°,求∠BDC的大小.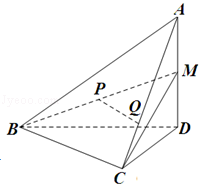
查看答案和解析>>
科目: 来源: 题型:解答题
如图,三棱柱ABC—A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
(1)求证:平面AA1B1B⊥平面BB1C1C;
(2)若AB=2,求三棱柱ABC—A1B1C1的体积.
查看答案和解析>>
科目: 来源: 题型:解答题
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1.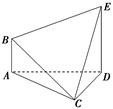
(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一结论;
(2)求多面体ABCDE的体积.
查看答案和解析>>
科目: 来源: 题型:解答题
如图甲,在平面四边形ABCD中,已知
 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
(1)求证:DC 平面ABC;
平面ABC;
(2)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com