
科目: 来源: 题型:单选题
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出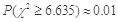 ,则下列说法正确的( )
,则下列说法正确的( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
查看答案和解析>>
科目: 来源: 题型:单选题
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
查看答案和解析>>
科目: 来源: 题型:单选题
有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如下表:
| 平均气温(℃) | ﹣2 | ﹣3 | ﹣5 | ﹣6 |
| 销售额(万元) | 20 | 23 | 27 | 30 |
 x+a的系数
x+a的系数 .则预测平均气温为﹣8℃时该商品销售额为( )
.则预测平均气温为﹣8℃时该商品销售额为( )查看答案和解析>>
科目: 来源: 题型:单选题
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,第1小组的频数为6,则报考飞行员的学生人数是 ( )
| A.36 | B.40 | C.48 | D.50 |
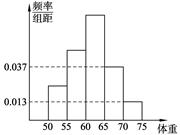
查看答案和解析>>
科目: 来源: 题型:单选题
某校五四演讲比赛中,七位评委为一选手打出的分数如下:
90 86 90 97 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A. | B. | C. | D. |
查看答案和解析>>
科目: 来源: 题型:单选题
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的中年职工为5人,则样本容量为( )
| A.7 | B.15 | C.25 | D.35 |
查看答案和解析>>
科目: 来源: 题型:解答题
(本题满分10分)《选修4-4:坐标系与参数方程》
在直接坐标系xOy中,直线 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为 ,判断点P与直线
,判断点P与直线 的位置关系;
的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目: 来源: 题型:解答题
(本题满分10分)选修4-4:坐标系与参数方程
已知曲线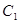 的极坐标方程是
的极坐标方程是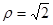 ,曲线
,曲线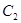 的参数方程是
的参数方程是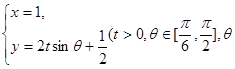 是参数).
是参数).
(1)写出曲线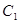 的直角坐标方程和曲线
的直角坐标方程和曲线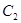 的普通方程;
的普通方程;
(2)求 的取值范围,使得
的取值范围,使得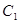 ,
,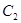 没有公共点.
没有公共点.
查看答案和解析>>
科目: 来源: 题型:解答题
在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的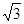 、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com