
科目: 来源: 题型:解答题
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
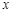 | 2 | 3 | 4 | 5 | 6 |
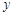 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目: 来源: 题型:解答题
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: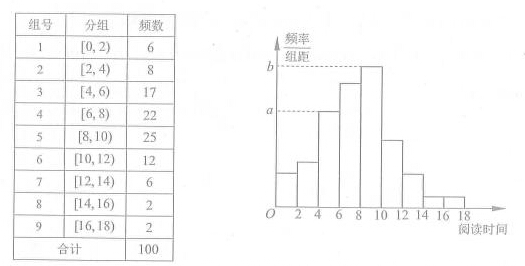
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
查看答案和解析>>
科目: 来源: 题型:解答题
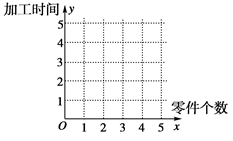
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数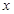 (个) (个) | 2 | 3 | 4 | 5 |
加工的时间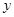 (小时) (小时) | 2.5 | 3 | 4 | 4.5 |
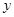 关于
关于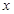 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;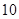 个零件需要多少时间?
个零件需要多少时间? ,其中
,其中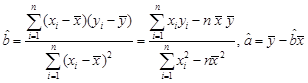 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
查看答案和解析>>
科目: 来源: 题型:解答题
对某校小学生进行心理障碍测试得到如下的列联表:
| | 有心理障碍 | 没有心理障碍 | 总计 |
| 女生 | 10 | | 30 |
| 男生 | | 70 | 80 |
| 总计 | 20 | | 110 |

| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:解答题
下表是某种产品销售收入与销售量之间的一组数据:
| 销售量x(吨) | 2 | 3 | 5 | 6 |
| 销售收入y(千元) | 7 | 8 | 9 | 12 |
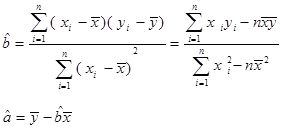
查看答案和解析>>
科目: 来源: 题型:解答题
某网站体育版块足球栏目组发起了“射手的连续进球与射手在场上的区域位置有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| | 有关系 | 无关系 | 不知道 |
| 40岁以下 | 800 | 450 | 200 |
| 40岁以上(含40岁) | 100 | 150 | 300 |
查看答案和解析>>
科目: 来源: 题型:解答题
巴西世界杯足球赛正在如火如荼进行.某人为了了解我校学生“通过电视收看世界杯”是否与性别有关,从全校学生中随机抽取30名学生进行了问卷调查,得到了如下列联表:
| | 男生 | 女生 | 合计 |
| 收看 | 10 | | |
| 不收看 | | 8 | |
| 合计 | | | 30 |
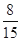 .
. 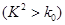 | 0.100 | 0.050 | 0.010 |
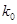 | 2.706 | 3.841 | 6.635 |
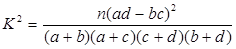 ,
, 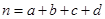 )
)查看答案和解析>>
科目: 来源: 题型:解答题
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如下图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个开学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量X的平均数和众数;
(2)将Y表示为X的函数;
(3)根据直方图估计利润不少于4800元的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某学校准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175以下(不包括175cm)定义为“不合格”
(1)求甲队队员跳高成绩的中位数
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取5人,则5人中“合格”与“不合格”的人数各为多少?
(3)从甲队178cm以上(包括178cm)选取2人,至少有一人在186cm以上(包括186cm)的概率为多少?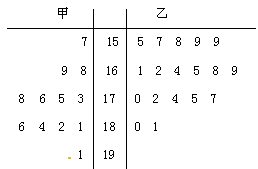
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com