
科目: 来源: 题型:解答题
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):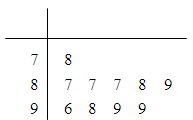
(1)指出这组数据的众数和中位数;
(2)若满意度不低于98分,则评价该教师为“优秀”.求从这10人中随机选取3人,至多有1人评价
该教师是“优秀”的概率;
(3)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记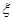 表示抽到评价该教师为
表示抽到评价该教师为
“优秀”的人数,求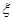 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。
(1)将 表示为
表示为 的函数;(2)根据直方图估计利润
的函数;(2)根据直方图估计利润 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损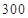 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t,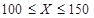 )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,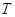 (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。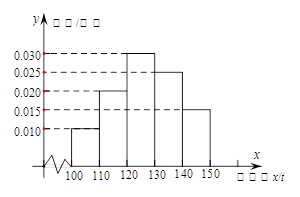
(1)将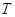 表示为
表示为 的函数;
的函数;
(2)根据直方图估计利润 不少于57000元的概率;
不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若 ,则取
,则取 ,且
,且 的概率等于需求量落入
的概率等于需求量落入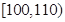 的概率),求利润
的概率),求利润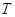 的数学期望.
的数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
从某校高二年级 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到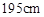 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组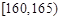 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
| 分组 | 频数 | 频率 | 频率/组距 |
| | | | |
 |  | 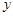 |  |
 |  |  |  |
| | | | |

 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率.查看答案和解析>>
科目: 来源: 题型:解答题
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
| | 患病 | 未患病 | 总计 |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | 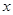 | 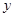 | 50 |
| 总计 | 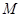 | 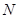 | 100 |
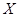 ;从服用药物的动物中任取两只,未患病数为
;从服用药物的动物中任取两只,未患病数为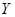 ,工作人员曾计算过
,工作人员曾计算过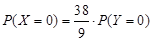 .
. 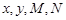 的值;
的值; 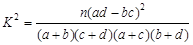 ,其中
,其中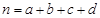 ;
; 、
、 有关联;
有关联; 、
、 有关联.
有关联.查看答案和解析>>
科目: 来源: 题型:解答题
为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |

| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目: 来源: 题型:解答题
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第五组 | (60,75] | 4 | 0.1 |
| 第六组 | (75,90) | 4 | 0.1 |
查看答案和解析>>
科目: 来源: 题型:解答题
某种报纸,进货商当天以每份1元从报社购进,以每份2元售出.若当天卖不完,剩余报纸报社以每份0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:份)的频率分布直方图(如图所示),将频率视为概率.
(1)求频率分布直方图中a的值;
(2)若进货量为n(单位:份),当n≥X时,求利润Y的表达式;
(3)若当天进货量n=400,求利润Y的分布列和数学期望E(Y)(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
科目: 来源: 题型:解答题
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组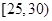 ,第2组
,第2组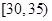 ,第3组
,第3组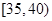 ,第4组
,第4组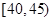 ,第5组
,第5组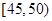 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.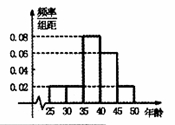

(1)求正整数 的值;
的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com