
科目: 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以 表示.
表示.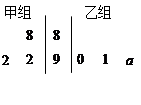
(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求 的值;
的值;
(Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;
(Ⅲ)当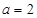 时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两名同学参加“汉字听写大赛”选拔性测试.在相同的测试条件下,两人5次测试的成绩(单位:分)如下表:
(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算);
(Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,求抽到的两个成绩中至少有一个高于
90分的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的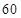 名候车乘客中随机抽取
名候车乘客中随机抽取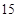 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 | 候车时间 | 人数 |
| 一 |  |  |
| 二 |  | 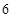 |
| 三 |  |  |
| 四 |  |  |
| 五 |  |  |
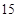 名乘客的平均候车时间;
名乘客的平均候车时间;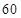 名乘客中候车时间少于
名乘客中候车时间少于 分钟的人数;
分钟的人数;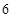 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.查看答案和解析>>
科目: 来源: 题型:解答题
 是指大气中直径小于或等于
是指大气中直径小于或等于 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即 日均值在
日均值在 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米
微克/立方米 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在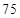 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 监测数据中随机的抽取
监测数据中随机的抽取 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
(1)在这 天的
天的 日均监测数据中,求其中位数;
日均监测数据中,求其中位数;
(2)从这 天的数据中任取
天的数据中任取 天数据,记
天数据,记 表示抽到
表示抽到 监测数据超标的天数,求
监测数据超标的天数,求 的分布列及数学期望;
的分布列及数学期望;
(3)以这 天的
天的 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
科目: 来源: 题型:解答题
根据空气质量指数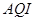 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
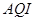 (数值) (数值) | 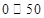 |  |  |  |  |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
 年
年 月
月 日—
日— 月
月 日,对空气质量指数
日,对空气质量指数 进行监测,获得数据后得到如图的条形图
进行监测,获得数据后得到如图的条形图
 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率; 个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.查看答案和解析>>
科目: 来源: 题型:解答题
根据空气质量指数 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
 (数值) (数值) | 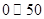 | 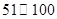 |  |  |  |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
 年
年 月
月 日—
日— 月
月 日,对空气质量指数
日,对空气质量指数 进行监测,获得数据后得到如图的条形图
进行监测,获得数据后得到如图的条形图
 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率; 个监测数据中任取
个监测数据中任取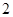 个,设
个,设 为空气质量类别颜色为紫色的天数,求
为空气质量类别颜色为紫色的天数,求 的分布列.
的分布列.查看答案和解析>>
科目: 来源: 题型:解答题
从某年级学生中,随机抽取50人,其体重(单位:千克)的频数分布表如下:
| 分组(体重) | 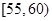 | 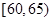 | 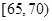 | 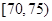 |
| 频数(人) | 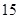 | 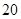 | 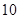 | 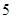 |
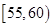 的频率;
的频率;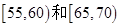 中共有几人?
中共有几人?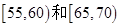 的人中,任取2人,求体重在
的人中,任取2人,求体重在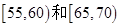 中各有1人的概率.
中各有1人的概率.查看答案和解析>>
科目: 来源: 题型:解答题
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢[来源:学科网ZXXK] | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中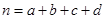 )
)查看答案和解析>>
科目: 来源: 题型:解答题
由某种设备的使用年限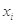 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得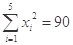 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的维修费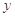 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与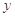 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中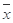 ,
, 为
为
样本平均值,线性回归方程也可写为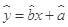 .
.
查看答案和解析>>
科目: 来源: 题型:解答题
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 | 候车时间 | 人数 |
| 一 |  | 2 |
| 二 |  | 6 |
| 三 |  | 4 |
| 四 |  | 2 |
| 五 |  | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com