
科目: 来源: 题型:解答题
为了调查某大学学生在周日上网的时间,随机对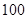 名男生和
名男生和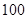 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) | 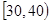 | 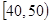 | 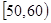 |  | 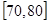 |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | 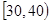 | 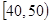 | 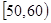 |  | 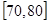 |
| 人数 | 10 | 20 | 40 | 20 | 10 |
 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
 ,其中
,其中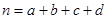
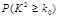 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
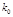 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目: 来源: 题型:解答题
南昌市为增强市民的交通安全意识,面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通,把符合条件的1000名志愿者按年龄分组:第1组 、第2组
、第2组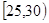 、第3组
、第3组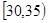 、第4组
、第4组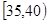 、第5组
、第5组 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者在五一节这天到广场协助交警维持交通,应从第3、4、5组各抽取多少名志愿者?
(2)在(1)的条件下,南昌市决定在这12名志愿者中在第四或第五组的志愿者中,随机抽取3名志愿者到学校宣讲交通安全知识,求到学校宣讲交通知识的资源者中恰好1名市第五组的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):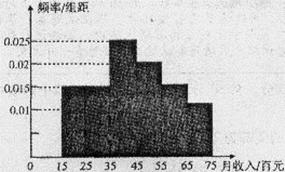
| 月收入(百元) | 赞成人数 |
| [15,25) | 8 |
| [25,35) | 7 |
| [35,45) | 10 |
| [45,55) | 6 |
| [55,65) | 2 |
| [65,75) | 1 |
查看答案和解析>>
科目: 来源: 题型:解答题
从某学校高三年级 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组 ; 第八组
; 第八组 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图. 
(1)根据已知条件填写下面表格:
| 组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 样本数 | | | | | | | | |
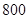 名学生中身高在
名学生中身高在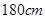 以上(含
以上(含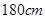 )的人数;
)的人数;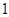 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有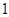 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7、8、9、10环,且每次射击成绩互不影响,射击环数的频率分布表如下: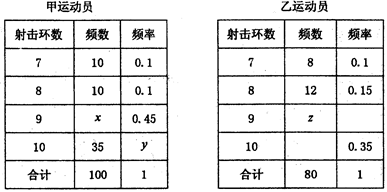
若将频率视为概率,回答下列问题:
(1)求表中x,y,z的值及甲运动员击中10环的概率;
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及
查看答案和解析>>
科目: 来源: 题型:解答题
南昌市为增强市民的交通安全意识,面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通,把符合条件的1000名志愿者按年龄分组:第1组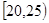 、第2组
、第2组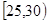 、第3组
、第3组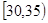 、第4组
、第4组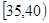 、第5组
、第5组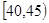 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者在五一节这天到广场协助交警维持交通,应从第3、4、5组各抽取多少名志愿者?
(2)在(1)的条件下,南昌市决定在这12名志愿者中随机抽取3名志愿者到学校宣讲交通安全知识,若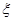 表示抽出的3名志愿者中第3组的人数,求
表示抽出的3名志愿者中第3组的人数,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
在某次测验中,有6位同学的平均成绩为76分,用 表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
(1)求第6位同学的成绩 及这6位同学成绩的标准差s;
及这6位同学成绩的标准差s;
(2)从6位同学中随机地选2位同学,求恰有1位同学成绩在区间(70,75)中的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.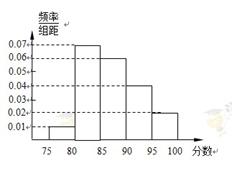
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
② 学校决定在这6名学生中随机抽取2名学生接受考官的面试,设第4组中有X名学生被考官面试,求X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:解答题
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组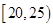 ,第2组
,第2组 ,第3组
,第3组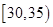 ,第4组
,第4组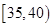 ,第5组
,第5组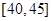 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目: 来源: 题型:解答题
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下: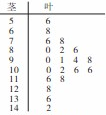
得到频率分步表如下:
(1)求表中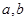 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在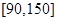 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com