
科目: 来源: 题型:解答题
、(本小题满分12分)某市统计局就某地居民的月收入调查了10000人,他们的月收入均在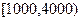 内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在 内)
内)
(1)求 某居民月收入在
某居民月收入在 内的频率;
内的频率;
(2)根据该频率分布直方图估计居民的月收入的中位数; (3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在
(3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在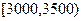 内的居民中抽取多少人?
内的居民中抽取多少人?
查看答案和解析>>
科目: 来源: 题型:解答题
、为加大西部开发步伐,国家支持西部地区选拔优秀“村官”深入农村开展工作,某市在2010年的“村官”选拔考试中随机抽取100名考生的成绩,按成绩分组,得到的频率分布表如下图所示:
(1)请先求出频率分布表中①、②位置的相应数据,再完成 下面的频率分布直方图;
下面的频率分布直方图;
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  | 5 | 0.05 |
| 第二组 |  | ① | 0.35 |
| 第三组 | 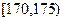 | 30 | ② |
| 第四组 |  | 20 | 0.20 |
| 第五组 |  | 10 | 0.10 |
| 合计 | 100 | 1.00 | |

 用分层抽样抽取6名考生进入第二轮面试,求第3,4,5组每组各抽取多少考生进入第二轮面试?
用分层抽样抽取6名考生进入第二轮面试,求第3,4,5组每组各抽取多少考生进入第二轮面试?查看答案和解析>>
科目: 来源: 题型:解答题
((本小题满分12分)
某学校准备购买一批电脑,在购买前进行的市场调查显示:在相同品牌、质量与售后服务的条件下,甲、乙两公司的报价都是每台6000元。甲公司的优惠条件是购买10台以上的,从第11台开始按报价的七折计算,乙公司的优惠条件是均按八五折计算。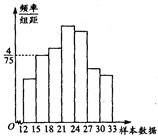
(1)分别写出在两公司购买电脑的总费用y甲、y乙与购买台数x之间的函数关系式;
(2 )根据购买的台数,你认为学校应选择哪家公司更合算?说明理由。
)根据购买的台数,你认为学校应选择哪家公司更合算?说明理由。
查看答案和解析>>
科目: 来源: 题型:解答题
(本小题满分12分)
如图,是总体的一样本频率分布直方图,且在[15,18)内频数为8。
(1)求样本容量;
(2)若在[12,15)内小矩形面积为0.06,求在[12,15)内的频数;
(3)求样本[18,33]内的频率。
查看答案和解析>>
科目: 来源: 题型:解答题
某校组织一次篮球投篮测试,已知甲同学每次投篮的命中率均为1/2。
(1)若规定每投进1球得2分,甲同学投篮4次,求总得分X的概率分布和数学期望。
(2)假设连续3次投篮未中或累计7次投篮未中,则停止投篮测试,问:甲同学恰好投篮10次,被停 止投篮测试的概率是多少?
止投篮测试的概率是多少?
查看答案和解析>>
科目: 来源: 题型:解答题
某班主任对班级22名学生进行了作业量多少的调查,数据如下:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
(Ⅰ)根据以上数据建立一个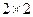 列联表;
列联表;
(Ⅱ)试问喜欢电脑游戏与认为作业多少是否有关系?
(可能用到的公式: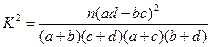 ,可能用到数据:
,可能用到数据: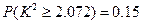 ,
,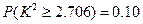 ,
, ,
, .)
.)
查看答案和解析>>
科目: 来源: 题型:解答题
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],……,(510,515],由此得到样本的频率分布直方图,如图4所示.根据频率分布直方图,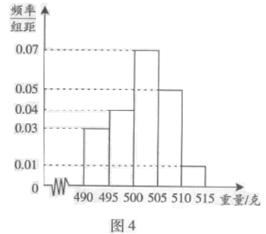
求(1)重量超过500 克的产品的频率;
(2)重量超过500 克的产品的数量.
查看答案和解析>>
科目: 来源: 题型:解答题
.(本小题满分12分)
为了调查某中学高三学生的身高情况,在该中学高三学生中随机抽取了40名同学作为样本,测得他们的身高后,画出频率分布直方图如下:
(I)估计该校高三学生的平均身高;
(II)从身高在180cm(含180cm)以上的样本中随机抽取2人,记身高在185~190cm之间的人数为X,求X的分布列和数学期望。
查看答案和解析>>
科目: 来源: 题型:解答题
(13分)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目: 来源: 题型:解答题
(13分)
某研究机构为了研究人的脚的大小(码)与身高(厘米)之间的关系,随机抽测了20人,得到如下数据:
| 序号 | 身高x | 脚长y | 序号 | 身高x | 脚长y |
| 1 | 176 | 42 | 11 | 179 | 44 |
| 2 | 175 | 44 | 12 | 169 | 43 |
| 3 | 174 | 41 | 13 | 185 | 45 |
| 4 | 180 | 44 | 14 | 166 | 40 |
| 5 | 170 | 42 | 15 | 174 | 42 |
| 6 | 178 | 43 | 16 | 167 | 42 |
| 7 | 173 | 42 | 17 | 173 | 41 |
| 8 | 168 | 40 | 18 | 174 | 42 |
| 9 | 190 | 46 | 19 | 172 | 42 |
| 10 | 171 | 42 | 20 | 175 | 41 |
| | 高个 | 非高个 | 合计 |
| 大脚 | | | |
| 非大脚 | | 12 | |
| 合计 | | | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com