．［必做题］（本小题满分10分）
已知，（其中）
.
(1)求；
(2)求证：当时，．

若 ，
试求；

已知名学生和名教师站在一排照相，求:
（1）中间二个位置排教师，有多少种排法？
（2）首尾不排教师，有多少种排法？
（3）两名教师不能相邻的排法有多少种？

（本小题满分12分）求证：3²ⁿ⁺²-8n–9（n∈N*）能被64整除．

（本小题满分12分）
已知展开式中第三项的系数比第二项的系数大162，求：
（1）的值；
（2）展开式中含的项.

(本题满分10分)
已知二项展开式中，第4项的二项式系数与第3项的二项式系数的比为.
（I）求的值；
（II）求展开式中项的系数。

（本小题满分12分）已知f (x)＝(1＋x)^m＋(1＋2x)ⁿ(m，n∈N^*)的展开式中x的系数为11.
(1)求x²的系数的最小值；
(2)当x²的系数取得最小值时，求f (x)展开式中x的奇次幂项的系数之和．
解： (1)由已知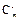＋2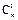＝11，∴m＋2n＝11，x²的系数为
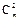＋2²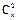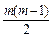＝＋2n(n－1)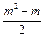＝＋(11－m)(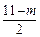－1)＝(m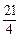－)²＋.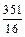
∵m∈N^*，∴m＝5时，x²的系数取最小值22，此时n＝3.
(2)由(1)知，当x²的系数取得最小值时，m＝5，n＝3，
∴f (x)＝(1＋x)⁵＋(1＋2x)³.设这时f (x)的展开式为f (x)＝a₀＋a₁x＋a₂x²＋^…＋a₅x⁵，
令x＝1，a₀＋a₁＋a₂＋a₃＋a₄＋a₅＝2⁵＋3³，
令x＝－1，a₀－a₁＋a₂－a₃＋a₄－a₅＝－1，
两式相减得2(a₁＋a₃＋a₅)＝60， 故展开式中x的奇次幂项的系数之和为30.

（本小题满分12分）
已知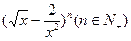的二项展开式中第五项的系数与第三项的系数的比是10：1.
（1）求二项展开式中各项系数的和；
（2）求二项展开式中系数最大的项和二项式系数最大的项

已知二项式的展开式中各项系数的和为64．
（I）求n；
（II）求展开式中的常数项．

（本小题满分12分）已知二项式的展开式中，前三项系数的绝对
值成等差数列．
（I）求展开式的第四项；
（II）求展开式的常数项.