某企业主要生产甲、乙两种品牌的空调，由于受到空调在保修期内维修费等因素的影响，企业生产每台空调的利润与该空调首次出现故障的时间有关，甲、乙两种品牌空调的保修期均为3年，现从该厂已售出的两种品牌空调中各随机抽取50台，统计数据如下：

品牌	甲				乙
首次出现故障时间 x年
空调数量（台）	1	2	4	43	2	3	45
每台利润（千元）	1	2	2.5	2.7	1.5	2.6	2.8

春节期间，某商场决定从3种服装、2种家电、3种日用品中，选出3种商品进行促销活动。
⑴)试求选出的3种商品中至少有一种是家电的概率；
⑵商场对选出的某商品采用抽奖方式进行促销，即在该商品现价的基础上将价格提高100元，规定购买该商品的顾客有3次抽奖的机会：若中一次奖，则获得数额为元的奖金；若中两次奖，则共获得数额为元的奖金；若中3次奖，则共获得数额为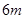元的奖金。假设顾客每次抽奖中获的概率都是，请问：商场将奖金数额m最高定为多少元，才能使促销方案对商场有利？

甲乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为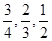，乙队每人答对的概率都是．设每人回答正确与否相互之间没有影响，用表示甲队总得分．
（I）求随机变量的分布列及其数学期望E；
（Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．

一个袋中装有大小相同的黑球和白球共9个，从中任取2个球，记随机变量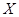为取出2球中白球的个数，已知．
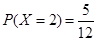（Ⅰ）求袋中白球的个数；
（Ⅱ）求随机变量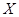的分布列及其数学期望．

袋中装着分别标有数字1，2，3，4，5的5个形状相同的小球.
（1）从袋中任取2个小球，求两个小球所标数字之和为3的倍数的概率；
（2）从袋中有放回的取出2个小球，记第一次取出的小球所标数字为x，第二次为y，求点满足的概率．

某停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过1小时收费6元，超过1小时的部分每小时收费8元（不足1小时按1小时计算）．现有甲、乙两人在该场地停车，两人停车都不超过4小时．
（Ⅰ）若甲停车1小时以上且不超过2小时的概率为，停车付费多于14元的概率为，求甲停车付费6元的概率；
（Ⅱ）若甲、乙两人每人停车的时长在每个时段的可能性相同，求甲乙二人停车付费之和为28元的概率．

x的取值范围为[0，10]，给出如图所示程序框图，输入一个数x．求：
（Ⅰ）输出的x（x＜6）的概率；
（Ⅱ）输出的x（6＜x≤8）的概率．

袋中又大小相同的红球和白球各1个，每次任取1个，有放回地摸三次．
（Ⅰ）写出所有基本事件‘
（Ⅱ）求三次摸到的球恰有两次颜色相同的概率；
（Ⅲ）求三次摸到的球至少有1个白球的概率．

在乒乓球比赛中，甲与乙以“五局三胜”制进行比赛，根据以往比赛情况，甲在每一局胜乙的概率均为 ．已知比赛中，乙先赢了第一局，求：
(Ⅰ)甲在这种情况下取胜的概率；
(Ⅱ)设比赛局数为X，求X的分布列及数学期望（均用分数作答）。

一纸箱中放有除颜色外，其余完全相同的黑球和白球，其中黑球2个，白球3个.
（Ⅰ）从中同时摸出两个球，求两球颜色恰好相同的概率；
（Ⅱ）从中摸出一个球，放回后再摸出一个球，求两球颜色恰好不同的概率.